Была опубликована интересная статья на русском "Эффективные версии теоремы Эрдёша Винтнера" Ж. Тененбома , Ж. Вервеа по данной теме
https://www.researchgate.net/publicatio ... ber_TheoryСделаю небольшой обзор этой статьи.
Статья **"Эффективные версии теоремы Эрдёша–Винтнера"** (авторы: Ж. Тененбаум и Ж. Верве) посвящена изучению предельных распределений вещественных аддитивных арифметических функций. Основное внимание уделяется получению **эффективных оценок** для остаточных членов в теореме Эрдёша–Винтнера, а также исследованию скорости сходимости к нормальному распределению.
### Основные моменты статьи:
1. **Теорема Эрдёша–Винтнера**:
- Классическая теорема Эрдёша–Винтнера даёт критерий существования предельного распределения для вещественной аддитивной арифметической функции

. Условия теоремы включают сходимость рядов:

.
- Предельное распределение может быть дискретным, непрерывным сингулярным или абсолютно непрерывным.
2. **Эффективные оценки**:
- Основная цель статьи — получение **эффективных оценок** для равномерной нормы разности между эмпирической функцией распределения

и предельной функцией распределения

:

.
- В статье доказаны две теоремы:
- **Теорема 1.1**: Для случая, когда предельное распределение дискретно.
- **Теорема 1.2**: Для случая, когда предельное распределение непрерывно.
3. **Скорость сходимости**:
- В статье явно рассматривается **скорость сходимости** к нормальному распределению. Например, в **Теореме 1.2** даётся оценка:

,
где

— функция концентрации,

и

— параметры, зависящие от функции

и

.
- В **Теореме 1.3** рассматривается случай условного распределения, где также даются оценки скорости сходимости.
4. **Примеры**:
- В статье приведены примеры, иллюстрирующие полученные результаты. Например, для функции

показано, что скорость сходимости зависит от параметра
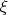
.
5. **Методы**:
- Основной метод доказательства — применение **теоремы 2.1** (из предыдущей работы Тененбаума), которая даёт эффективные оценки для средних значений комплексных мультипликативных функций.
- Также используются методы теории вероятностей, включая неравенство Берри–Эссеена для оценки скорости сходимости.
### Выводы:
- В статье **говорится о скорости сходимости** к предельному распределению. Авторы получают явные оценки для остаточных членов, которые зависят от параметров функции

и

.
- Результаты статьи позволяют лучше понять, как быстро эмпирическое распределение

сходится к предельному распределению

в зависимости от свойств аддитивной функции

.
В статье "Эффективные версии теоремы Эрдёша–Винтнера" явно не формулируются условия, при которых предельное распределение аддитивной арифметической функции

является нормальным.
Вот еще небольшой обзор работ на данную тему:
### 1. **[2] De la Bretèche R., Tenenbaum G. "Sur la concentration de certaines fonctions additives" (2012)**:
- **Основная тема**: В этой работе изучается **концентрация распределений** аддитивных арифметических функций. Авторы исследуют, как значения аддитивных функций группируются вокруг своего среднего значения.
- **Ключевые результаты**:
- Получены оценки для функции концентрации

, которая измеряет, насколько вероятно отклонение значений функции от среднего на величину

.
- Показано, что для некоторых классов аддитивных функций концентрация распределения близка к нормальной.
- **Связь с нормальным распределением**: Работа предоставляет инструменты для анализа близости распределения к нормальному, хотя прямое утверждение о нормальности не формулируется.
### 2. **[6] Erdős P., Kátai I. "On the concentration of distribution of additive functions" (1979)**:
- **Основная тема**: В этой статье исследуется **концентрация распределений** аддитивных функций. Авторы изучают, как значения аддитивных функций группируются вокруг своего среднего значения.
- **Ключевые результаты**:
- Получены оценки для функции концентрации

.
- Показано, что для широкого класса аддитивных функций распределение значений близко к нормальному.
- **Связь с нормальным распределением**: Работа подчёркивает, что для многих аддитивных функций предельное распределение близко к нормальному, особенно если функция удовлетворяет определённым условиям на простых числах.
### 3. **[9] Koukoulopoulos D. "On the concentration of certain additive functions" (2014)**:
- **Основная тема**: В этой работе изучается **концентрация распределений** аддитивных функций. Автор рассматривает функции, которые принимают малые значения на простых числах.
- **Ключевые результаты**:
- Получены точные оценки для функции концентрации

.
- Показано, что для функций, которые медленно растут на простых числах, распределение значений близко к нормальному.
- **Связь с нормальным распределением**: Работа явно связывает концентрацию распределения с нормальным законом для функций,
которые удовлетворяют условиям теоремы Эрдёша–Каца.### 4. **[11] Ruzsa I.Z. "On the concentration of additive functions" (1980)**:
- **Основная тема**: В этой статье исследуется **концентрация распределений** аддитивных функций. Автор изучает, как значения аддитивных функций группируются вокруг своего среднего значения.
- **Ключевые результаты**:
- Получены оценки для функции концентрации

.
- Показано, что для широкого класса аддитивных функций распределение значений близко к нормальному.
- **Связь с нормальным распределением**: Работа подчёркивает, что для многих аддитивных функций предельное распределение близко к нормальному, особенно если функция удовлетворяет определённым условиям на простых числах.
В указанных статьях явно не формулируются условия, при которых предельное распределение аддитивной арифметической функции

является нормальным.