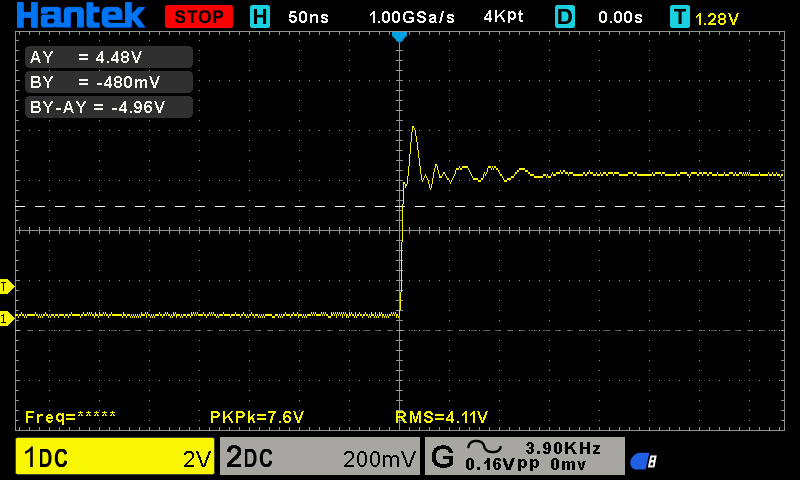
sergey zhukovrealeugeneСпасибо! Собственно, включив на щупе делитель 1:10 и выключив в осциллографе фильтр на 20МГц (ранее я забыл его выключить

), я, видимо, получил то, что хотел увидеть:
 -- 17.01.2025, 20:00 --
-- 17.01.2025, 20:00 --Это из какого учебника вы почерпнули подобную мудрость?
Из телеграфных уравнений, в предположении, что источник сигнала имеет гармонический вид, можно получить, что

.

и

здесь - погонные параметры. Погонная индуктивность есть вообще у любого проводника, поскольку ток, проходящий через этот проводник, создаст магнитное поле. Погонная емкость тоже есть, поскольку между любыми двумя проводящими областями существует какая-то емкость. Получается, что любой проводник характеризуется каким-то волновым сопротивлением



