Пытаюсь разобраться и найти объяснения тому, как распространяется сигнал от одного конца провода к другому. То есть, то, как растет потенциал с конца провода при подаче с другого конца постоянного напряжения.
Если рассматривать провод как длинную линию с распределенными параметрами, то получается следующая модель:
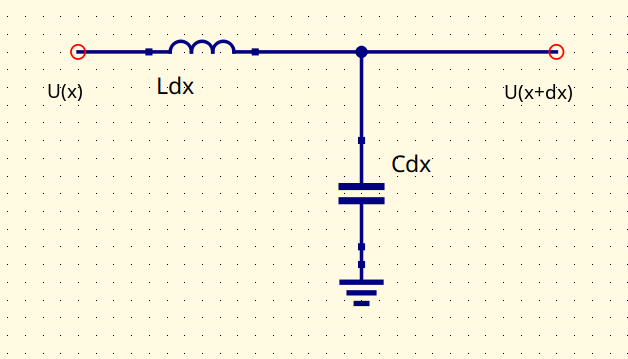
Которая приводит к телеграфным уравнениям:

Что в конечном счете приводит к волновому уравнению:

Если к границе подключен резистор

, то для границы будет выполняться:

. То есть, если подставить в первое телеграфное уравнение, то получим:

Казалось бы, вот то что нужно для численного решения. Но если подставить во второе уравнение, то получается:

А это приводит к противоречию:

Т.к. нагрузку можно подключать какую угодно, а вот

и

- параметры, определяющие только провод. Они не должны быть связаны с нагрузкой.
Что тут не так?