Если Вы про систему линейных однородных уравнений, то требование её разрешимости -- это равенство определителя нулю
Это понятно, я про вот это:
Думаю, что все крепления жёсткие, а углы стержней с осями вращения, по-хорошему, должны быть даны. Считайте, что они равны

.
Я использую вместо этих углов углы между вертикалью и стержнями, и обозначаю их

и

. Я так понимаю, что они не должны меняться со временем и они параметры.
При изучении динамики, они уже функции времени
Углы отклонения в плоскости колебаний у меня были как

. Они меняются со временем. Вопрос в том, в ответе имеется ввиду под

и

то что имею ввиду я, или так обозначены

. Если второе, то как мне тогда найти какие изначальные углы отклонения по вертикали у каждого маятника.
Ось

на рисунке drzewo это ось вращения массы m. То есть, Вы сначала поворачиваете массу 3m относительно её оси, а затем всю систему относительно оси вращения массы m, на рисунке это

.
Тут я окончательно запутался

. Верхний маленький стержень, который горизонтален, вдоль которого ось Oy, это вроде ось вращения массы 3m. Так как масса m с ним связана, то можно считать что масса m тоже может вращаться по этой оси. Чисто для массы m ось вращения это второй маленький стержень.
Похоже я до сих пор не понял кинематику задачи, поэтому уточню ее так:
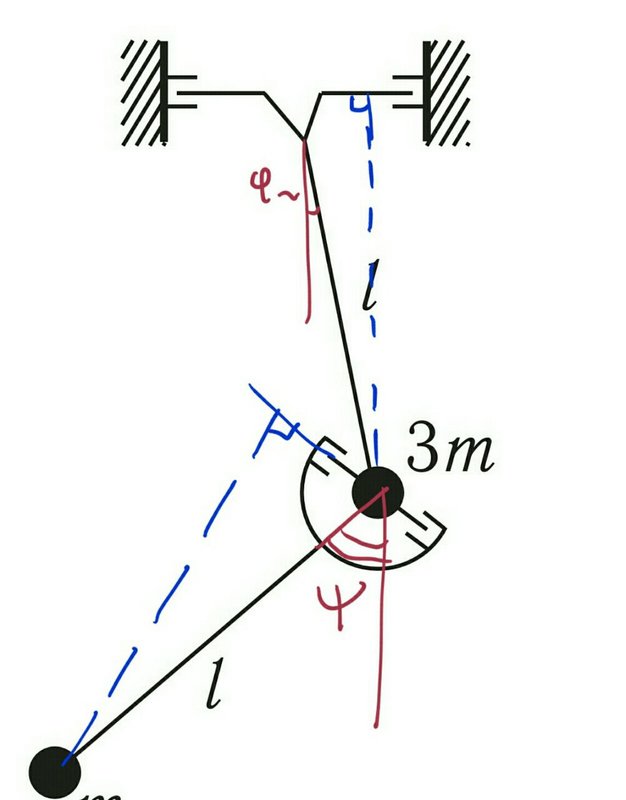
Синим я обозначил пересечение плоскости рисунка с плоскостями вращения шаров. Если я правильно понимаю, это есть те образующие конуса о которых Вы говорили.
Бардовый (это же бардовый ?) цвет обозначает вертикаль, и угол между вертикалью и большими стрежнями.