Теория "колыбели Ньютона"

[sergey zhukov]

manul91
Вот так это примерно выглядит:

Кинетическая энергия восстанавливается с точностью до 1,3% в этом расчете (с поправкой на то, что она выросла на 0,85% "просто так" из-за ошибок вычисления).

manul91 в сообщении #1667872 писал(а):

только одним свойством

Может быть. То, что волна не расплывается в этой модели при распространении по сплошной пружине - это точно известно (конкретный расчет, правда, ее размазывает, но это не дефект модели). Положим, стержень полубесконечный, и волна идет из бесконечности к концу, к которому приставлен отрезанный кусочек стержня. Она входит в этот кусочек, положим, "не замечая" разреза, и этот кусочек, положим, тут же отделяется. Стержень "избавился от колебаний". А что с кусочком, который отскочил? Свободен ли он от колебаний? Это не очевидно, но видимо, да (в специальном случае, конечно, когда волна была возбуждена ударом такого же кусочка с другой стороны). Дискретная модель примерно это показывает, если считать, что главная ошибка вносится дискретным приближением:

amon в сообщении #1667553 писал(а):

drzewo
Некоторое (большое) количество лет назад у нас на семинаре рассказывали как стержни сталкиваются плоскими торцами. Там задача теории упругости сводится к одномерной и, при небольшой помощи шаманского бубна, точно решается. В том числе, показывается, что для составного стержня из одинаковых кусочков отлетает один, если на эту байду налетает еще один такой же кусочек. Я сейчас пытался найти публикацию автора (вроде, он это где-то публиковал), но сходу не нашел.

Причем, видимо, стержень этот вообще может не работать на растяжение, т.е. это может быть стопка листов. Т.е. сплошной стержень и стержень из стопки листов - это в данной задаче одно и то же. Напряжения растяжения тут нигде не возникают. Поэтому в качестве "передающей среды" подходят и склеенные/не склееные шарики (тут, правда, неоднородность "линии" по длине нарушает идеальные условия "передачи волны без расплывания"), и сплошной стержень, и стопка пластин. Нужна лишь "согласованность входного/выходного сопротивления" этой линии с теми бьющими/отделяющимися частями с двух ее сторон.

Geen
Даже точно известно, что эти вычисления неустойчивы. Явная схема, и нет демпфирования. Например, суммарная энергия системы возрастает во времени линейно. За время этого вычисления она выросла примерно на 1%. Я не старался обеспечивать устойчивость.

[sergey zhukov]

Примерно так это происходит:

Здесь это выглядит несколько сложнее из-за остаточных колебаний, а в точном непрерывном решении все совсем просто.

В этой задаче существует всего два состояния пружины (или напряжения в материале) - сжато (на фиксированную величину) и расслаблено. Никаких других состояний нет. "Волна сжатия" представляет собой прямоугольную волну, внутри которой плотность материала повышена на фиксированную величину, а за ее пределами - сразу падает до плотности несжатого материала. Так что тут очень простая волна типа "есть/нет". На растяжение материал не работает.

Эта "волна сжатия" возникает в точке соударения пружин и "растет" в обе стороны по обеим пружинам . Когда она достигает левого конца ударной пружины, то перестает расти и начинает перемещаться по "передающей пружине" вправо в виде прямоугольной волны сжатия (там, где ее нет, состояние пружин становится расслабленным). Когда она достигает конца "отлетающей" пружины, то начинает уменьшаться, "втягиваясь" в точку будущего разрыва. Когда она полностью "втягивается" и все пружины снова находятся в расслабленном состоянии, происходит отрыв.

Похоже, вот тут речь была об этом:

wrest в сообщении #1667433 писал(а):

1. "Волна деформации": идёт в обе стороны от места удара, отражается от концов вереницы шаров и сходится ровно на границе между вторым и третьим шаром слева.

Т.е. волна деформации в случае одного ударного шара просто вдвое короче, чем в случае двух ударных шаров. Поэтому и на той стороне точка отрыва отстоит от того конца вдвое дальше.

Снизу для наглядности начальное состояние системы, чтобы было видно, насколько вся она перемещается вправо.

[manul91]

sergey zhukov
Совершенно согласен со всем что вы написали, включая "прямоугольной волной сжатия" и т.д.
Интересно насколько можно ослабить условия:
Когерентность передачи волны в стержне: насколько я понимаю это сводится к тому чтобы скорость передачи волн всех частот в стержне $u$ была одна и та же, плюс суперпозиции (т.е. классическое волновое решение). Притом ясно что прямоугольной волной сжатия дозволено как-то "деформироваться" в пути, если она выйдет к другом конце все же неизмененной т.е. такой как на "входе". Т.е. скорость звука ("коеффициент жесткости"?) может меняться по протяжение стержня типа зависимость $u(x)$, пока "свойство когерентности" сохраняется.
Согласованность налетающего и отскакивающего кусочка с друг другом (и самого стержня): Вроде очевидно что если они одинаковы (и одинаковы с материалом стержня т.е. "куски того же стержня") то все работает. А если нет?
Тыча пальцем в небо, я бы сказал так: нужно чтобы массы налетающего и отскакивающего куска были одинаковы. Еще нужно чтобы для них выполнялось то же требование "когерентности" что и для стержня, и "на стыке" со стержнем все было непрерывно. Т.е. если бы это изначально был единый "когерентный стержень" (скорость звука может быть разной в разных мест, меняясь непрерывно на протяжение стержня) и мы с обоих сторон отрезали кусочков одинаковой массы - то все наверно сработает (возможно останутся какие-то волны в улетающего куска, если он не идентичен налетающего распределением скорости звука по своей длине).
Хорошо бы конечно расписать все это в какой-то математической форме, только мне не совсем понятно как.

[sergey zhukov]

manul91
Я еще подумал, что все проще анализировать, если нарисовать продольные колебания, как поперечные. Даже просто заменить продольные на поперечные, это в нашем случае практически одно и то же. Вот струна со свободными концами, причем начальные условия такие, что первые четыре левых сегмента имеют одинаковую вертикальную скорость (момент удара пружинки), а все остальные сегменты неподвижны:

Такие начальные условия приводят к формированию "волны плотности" (наклонный участок, который бежит по струне слева-направо), который вдвое длиннее участка с ненулевой начальной скоростью, т.е. восемь сегментов. Причем в непрерывной однородной модели этот наклонный участок при таких начальных условиях должен быть просто бегущей прямой линией с четкими углами. Тут же он только к этому приближается.

Когда этот участок доходит до конца, он "вращается" вокруг своего заднего угла и "выгибается". Здесь он теряет свою прямую форму, поскольку тут фактически накладываются друг на друга прямая и отраженная волны. Когда он "перевернулся" и "выпрямился", то начинается бег в обратную сторону и так множество раз.

Здесь все сегменты соединены друг с другом двухсторонними связями. Но если концевой участок из четырех сегментов может быть только тянутым, но не может тянуть сам (одностороннее соединение, т.е. "шарик прислонен, но не приклеен"), то в момент полного выпрямления струны он просто отделяется:

Пока волна идет слева направо и "вращается" на конце до выпрямления, в этой задаче достаточно одностороннего соединения всех сегментов, результат будет совершенно тот же (происходит только сжатие). Но как только произошло выпрямление, дальше должна формироваться обратная волна растяжения, которая пойдет в обратную сторону. Если есть точка, в которой растяжение в принципе не может существовать, то в этом месте произойдет отделение.

Вообще понятно, что начальные условия на левом конце струны точно воспроизводятся на ее правом конце, т.е. при повторном выпрямлении четыре последних сегмента имеют вертикальные скорости, а остальные неподвижны. Это значит, что задача обращается: все напряжения сжатия заменяются на напряжения растяжения и все проигрывается с обратного конца. Первая точка, где должны возникнуть напряжения растяжения - это точка, "зеркальная" той, где первыми возникают напряжения сжатия в "прямом проходе", т.е. место удара. Поэтому тут и происходит отделение.

[Geen]

sergey zhukov в сообщении #1667884 писал(а):

Даже точно известно, что эти вычисления

Тогда Вы понимаете, что ценность этих картинок околонулевая? но продолжаете их постить в больших количествах...

[sergey zhukov]

Вот так выглядит "столкновение двух струн", аналогичное столкновению двух пружинок:


Geen
Люблю картинки, особенно где все движется. Даже неправильные. Ничего не могу с собой поделать.

[EUgeneUS]

Geen в сообщении #1668020 писал(а):

Тогда Вы понимаете, что ценность этих картинок околонулевая?

Не согласен, что "околонулевая".
Хотя да, отсутствие устойчивости снижает ценность - приходится держать в голове, что какие-то особенности поведения могут оказаться не результатом примененной модели, а артефактами расчетов.

[мат-ламер]

Geen в сообщении #1668020 писал(а):

Тогда Вы понимаете, что ценность этих картинок околонулевая? но продолжаете их постить в больших количествах..

Не согласен. Для форума самое то. Кому-то может интересны теоретические дискуссии (типа, можно ли делить на ноль? ). А лично мне интересны картинки.
sergey zhukov
Выражаю благодарность!

[manul91]

sergey zhukov
Понятно что схема неустойчива; если например вдвое уменьшить дискретизацию рассчетов (в пространстве и времени) - то как это скажется на рост оценки суммарной ошибки по небаланса энергии (уменьшит, увеличит, останется такой же)?
Также любопытно поведение в таких случаев "отката"/"качели", когда коеффициент жесткости плавно меняется по протяжении струн/стержней...

[sergey zhukov]

Вот, кстати, точное решение:


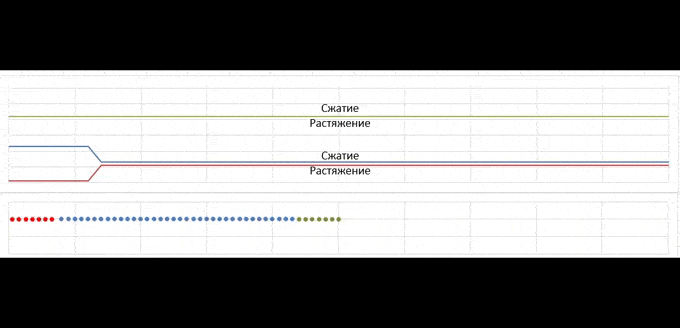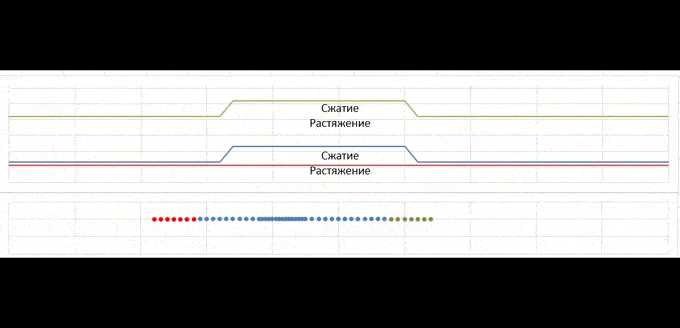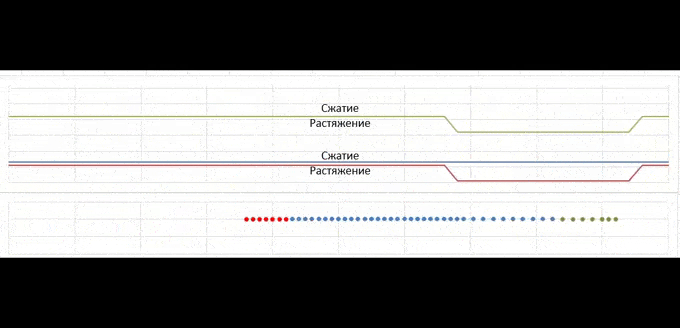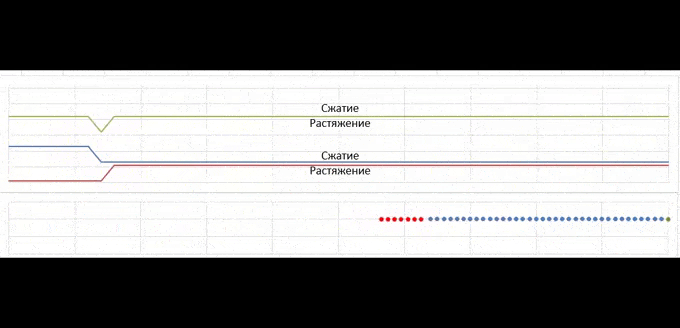
Здесь все начинается с момента удара красной пружинки слева (движется слева направо), причем после удара она приклеивается. А аналогичный зеленый сегмент справа тоже приклеен (это чтобы можно было видеть несколько проходов волны).

На графиках нарисована волна деформации (вверх - сжатие, вниз - растяжение). Внизу нарисована она же, но в виде разложения на волну, бегущую направо (сжатие) и налево (растяжение). Когда волна сжатия добегает до конца пружины, она отражается, как волна растяжения (и наоборот) и так бегает по кольцу. Сумма этих волн дает верхний результат. Снизу приведено движение сборки после удара по типу гусеницы.

Как видно, волна сжатия/растяжения прямоугольная (фронты на самом деле вертикальные). Импульс частиц меняется только на границе волны, а внутри и вне волны скорости частиц постоянны. Из этого следует, что скорость частицы равна нулю только если и волна сжатия (прямая) и волна растяжения (обратная) (а не просто их сумма) в этой точке равны нулю.

Все начинается с того, что красный сегмент "приносит с собой" волну, сложенную на нем "пополам". Собственно, движущийся сегмент пружины можно представлять, как такой сегмент, по которому непрерывно циркулирует волна деформации длиной вдвое больше этого сегмента, т.е. ее начало совпадает с ее концом. Когда красный сегмент ударяется об остальную часть, он "выпускает" эту волну, и мы видим, что она захватывает вдове большую длину, чем длина красного сегмента. "Длина" в данном случае означает число точек, отмечающих равные расстояния на ненапряженной пружине. Понятно, что если деформации малы, как в колыбели Ньютона, то можно не думать о том, как волна деформации меняет расстояния между точками тела, по которому она идет, и просто говорить о том, что расстояние между точками не меняется. А если они велики, то эти вещи уже нужно различать.

Когда волна добегает до селеного сегмента и складывается там вдвое, он должен оторваться (если не приклеен). Отрыв должен произойти там, где первый раз в этой задаче появляется растяжение.

manul91
Руки пока не дошли до переменных параметров по длине. Но это мне тоже интересно. Просто там ничего такого простого не ожидается, ведь наверняка в переменной среде нет строгой "когерентности".
Конечно, измельчение пространственно-временной сетки уменьшает ошибку. Но по хорошему нужно просто правильно организовать расчет или применить более сложный метод численного решения. Например, я часто ввожу тут искусственную вязкость, которая поддерживает полную энергию системы на неизменном уровне.

[manul91]

sergey zhukov в сообщении #1668544 писал(а):

Руки пока не дошли до переменных параметров по длине. Но это мне тоже интересно. Просто там ничего такого простого не ожидается, ведь наверняка в переменной среде нет строгой "когерентности".

Если все что меняется по длине это только скорость звука, то как мне кажется, такое должно сохранять "когерентность" в необходимом смысле (разумеется в любой точке, скорость звука для всех частот должна оставаться одинаковой).
Интуитивно, если a) волна удара везде по пути с одного конца к другого оставалась бы волной сжатия (а не расширения), и б) сумела "вся войти" в кусок который только опирается на выходном конце - то "откат" имхо должен сработать так же

[sergey zhukov]

manul91
Из теории следует, что при нормальном падении на плоскость раздела фаз волна проходит без отражения только если акустические импедансы сред (произведение скорости звука на плотность среды) этих сред равны. Т.е. если мы имеем среду с плавным градиентом свойств таким, что акустический импеданс сохраняется, то, наверное, в некотором приближении можно считать, что волновой пакет не расплывается.

Да и то это, наверное, работает только если длина волны много меньше характерных масштабов изменения свойств, т.е. каждая волна локально находится в условиях квазипостоянных свойств среды. Скажем, если направить прямоугольный пакет на "согласованный" раздел фаз, то вряд-ли он прямо так и пройдет сквозь него без изменений и отражений.

[sergey zhukov]

Нашел тут одну книжку, где прямо ставится вопрос о том, как должны менятся параметры среды для безотражательного движения волны. Тут вначале речь о том, что общий подход в таких случаях - допущение о достаточно плавном изменении параметров (приближение). А дальше находятся специальные профили изменения параметров такие, для которых плавность уже не обязательна, все равно отражения не будет. Это все не так-то и просто оказывается.

[manul91]

sergey zhukov в сообщении #1669144 писал(а):

Нашел тут одну книжку, ..... Это все не так-то и просто оказывается.

Да довольно интересно, спасибо