Вот так выглядит столкновение одной массивной пружинки с группой из четырех последовательно поставленных других:
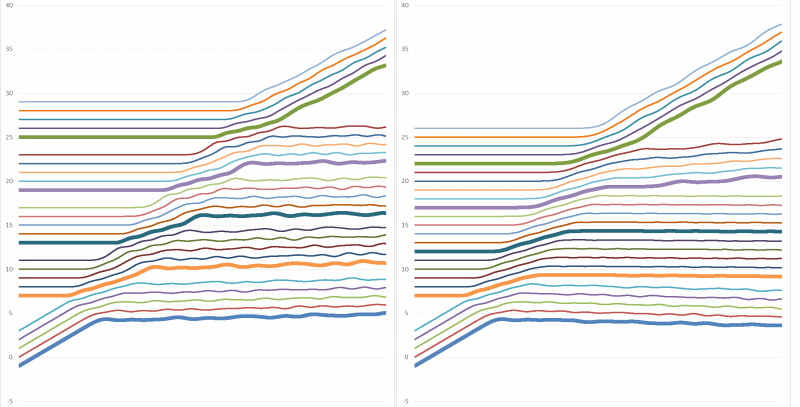
На первом рисунке - пружинки стоят с зазорами. На втором - без. Можно видеть, что все пружинки немного передвигаются, т.е. шарики не остаются строго неподвижными.
Вот так выглядит удар двух шариков (тоже с зазорами и без):
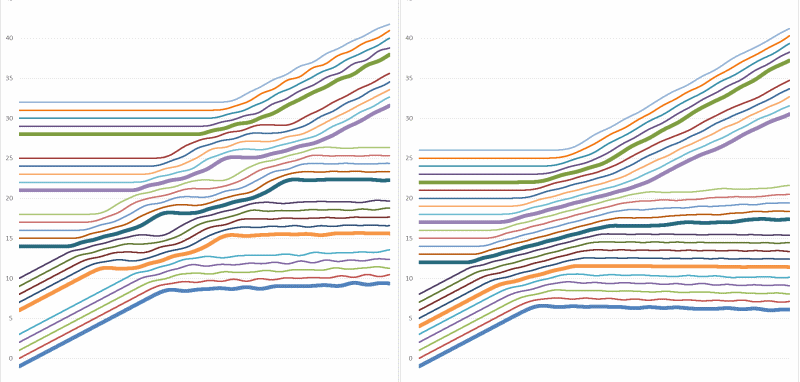
Видно, что зазоры делают решение более "идеальным", а "множественные столкновения" приводят к немного другой картинке (близкой, впрочем, к идеальной).
Интересно, что в этой модели склеивание всех промежуточных пружинок не приводит практически ни к каким последствиям. Решение становится даже еще более красивым:
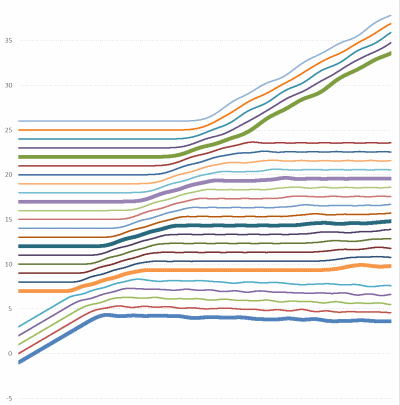
Т.е. в принципе вместо цепи шариков можно подвесить стержень, он будет передавать волну точно так же (только его нужно "согласовать" с входным и выходным шариками).
В модели абсолютно жестких тел удар легкого шарика по тяжелому стержню (только по нему) приводит к отскоку шарика и медленному движению стержня. Если с другой стороны стержня с зазором установлен такой же шарик, то он не отлетит симметрично удару первого шарика, разумеется. Т.е. тут "теория вставки зазоров" (даже бесконечно малых) говорит нам, что склейка всех промежуточных шариков все сломает. Однако если на другом конце стержня такой же шарик был прислонен до удара без зазора, то возникает неопределенность, которую однозначно нельзя разрешить без привлечения теории упругости (множественные столкновения), как тут выше уже правильно говорили. И выясняется, что на самом деле склейка шариков ничего не сломает (это, правда, только на одномерной однородной модели так, а с шариками все посложнее будет).