Метрика Шварцшильда описывает гравитационное поле сферического тела. Специальная теория относительности, основанная на преобразованиях Лоренца, экспериментально подтверждена. При слабой гравитации пространство-время приближенно плоское и метрика Шварцшильда в прямоугольных координатах в первом приближении принимает вид

При малой скорости, ускорения материальной частицы вдоль координат следуют из уравнений геодезических:


После преобразований Лоренца, когда наблюдатель движется вдоль координаты x, метрика принимает вид

при

и

. Выражения для ускорений вдоль пространственных координат и времени при малых

и

без величин большего порядка малости по сравнению с

будут

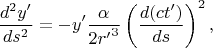


Этот результат может объяснить годовые изменения в дополнительном ускорении Пионера 10, см.
https://arxiv.org/pdf/gr-qc/9903024 [1],
https://arxiv.org/pdf/gr-qc/0104064.
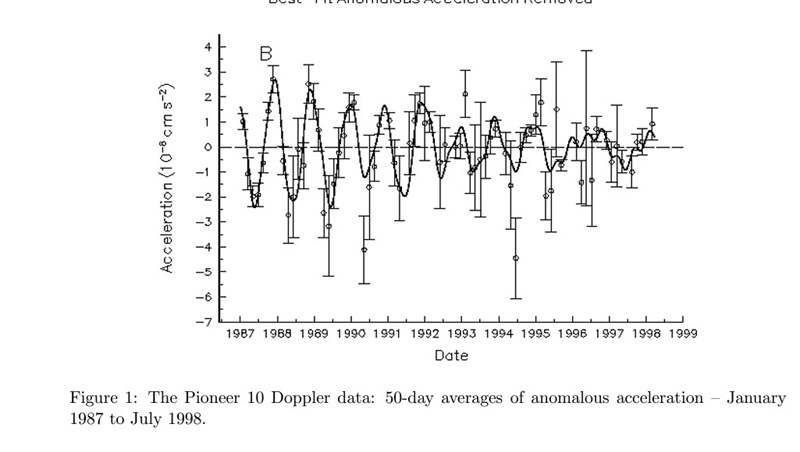
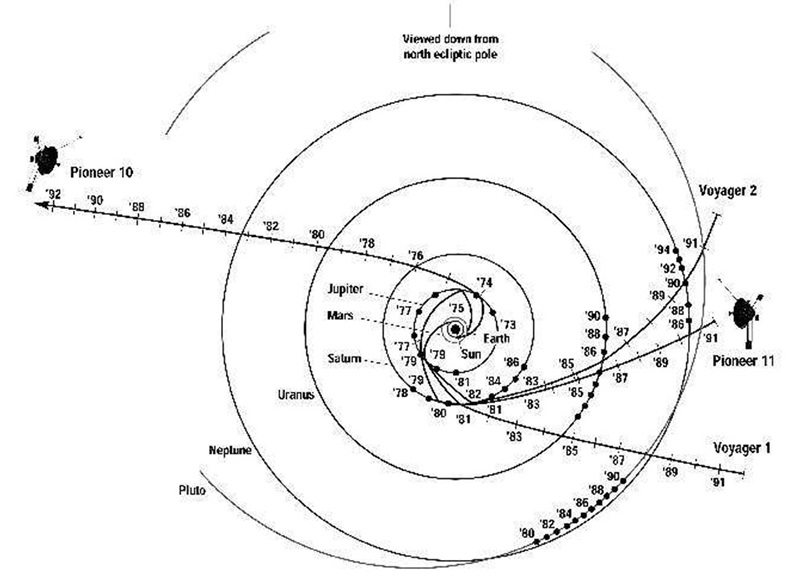
Рассмотрим ожидаемое дополнительное ускорение Pioneer 10, определенное с помощью эффекта Доплера. Оно имеет периодическую составляющую с амплитудой

на расстоянии 40 а.е. и

для 60 а.е. Ускорения и расстояния определяются приблизительно по графику и схеме полета.
Суммарное дополнительное ускорение определялось по формуле [1], связывающей расчетную частоту принятого сигнала с наблюдаемой,

в предположении, что это вызвано ускорением самого космического аппарата. Однако тот же эффект даст и замедление времени, рассчитанное по формуле

для

.
Направим ось X от Солнца к аппарату Pioneer 10. Скорость

вычисляется следующим образом:

где

— скорость Пионера относительно Солнца,

— орбитальная скорость Земли,

— период обращения Земли вокруг Солнца, а

— начальный угол. Расчеты с использованием формулы для

при преобразовании в ускорение для периодической составляющей дают

на расстоянии 40 АЕ и

для 60 АЕ. Эти значения близки к наблюдаемым.
Есть ли какие-нибудь другие наблюдения, подтверждающие этот результат?