Здраствуйте.
Решаю задачи из сборника и застряла вот на такой:
Collection of problems in advanced mathematics, Technion, 2011 писал(а):
Problem 10.109
For each
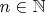
a body

in coordinate space is defined by the inequality

, and body

is the union of all bodies

.
Find the volume of the body

Я правильно понимаю, что нужно доказать, что

таких что

найдется такое

, что неравенство в условии выполняется? Или я что-то путаю?
Но в любом случае прежде чем приступать к доказательству, хотелось бы знать, какое это тело

? А это я даже представить себе не могу.
Можете подтолкнуть к решению?
И еще чисто технический вопрос. Могу ли я вот эту фразу:
Цитата:
body

is the union of all bodies

записать символически как

?
Ведь это символ обьединения множеств, а тут не множества, а какие-то пространственные тела.



