Окончательная добавка про рисование на спектре, просто "для полноты" предыдущего рассказа об этом:
- инопланетянский ответ на упоминавшееся выше <<послание "Вояджера">> (внимание, вопрос: что там? :) Для просмотра в упоминавшейся выше маткадной программке надо в ней выбрать значения Nfft=512 и Step=256.
Если исходная картинка цветная, то её следует редактором картинок сделать черно-белой: надо вывести в ноль параметр цветовой насыщенности. Файл с картинкой должен быть в формате bmp. Размер картинки в формате bmp по вертикали в пикселях надо обязательно сделать равным
двойке в целой степени. Размеры (обозначаю их как CxR) bmp-картинки будут важными параметрами:

- количество колонок, т.е. столбцов, это длина картинки по горизонтали в пикселях, и

- количество рядов, т.е. строк, это размер картинки по вертикали. Ниже для примера взята небольшая картинка, 356x256:
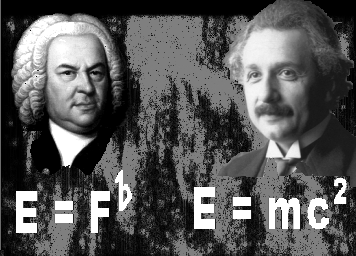
Десятый байт в заголовочной части bmp-файла указывает на смещение данных от начала файла. Обычно десятичное значение этого смещения равно

Каждый пиксель обычно описывается тремя байтами; из них будет нужен только один. Т.е. нужный нам одномерный массив данных

(однобайтовых, с целыми десятичными значениями от

до

выбирается из прочитанного Маткадом bmp-файла как последовательность байтов с номерами

где

Из этого массива строится двумерная таблица,

где

это номер ряда в картинке,

- номер столбца. В ней элементы каждого столбца интерпретируются как результат

дискретного преобразования Фурье (Complex Fast Fourier Transform, CFFT) выборки длиной

комплексного аудио сигнала

где

и

это стерео-каналы (в цифровой радиотехнике

и

интерпретируются как "синфазная" (inphase) и "квадратурная" (quadrature) составляющие двухканального iq-сигнала). Вернее, числа из

интерпретируем как модули

комплексных чисел

Предполагаем, что выборки берутся с перекрытием, т.е., например, с шагом

при длине выборок

В Маткаде операция

соответствует формуле:

Обратное преобразование

это

Элементы выходного массива операции CFFT в Маткаде пронумерованы так: сначала, при

идёт спектр с возрастающими от нуля положительными частотами, а дальнейшим номерам

соответствуют возрастающие отрицательные частоты, от (почти) с минусом половины частоты дискретизации до нулевой частоты. Чтобы получить обычную шкалу возрастающих частот, с нумерацией подряд от "левого конца" спектра до "правого конца" (т.е. "сверху вниз" на спектрограмме) с нулевой частотой по центру, приходится делать перенумерацию выходного массива. Перед операцией ICFFT надо аналогичным образом перенумеровывать входной массив.
Заодно пояснение к операции, изображаемой в Маткаде стрелкой над формулой: это просто краткая запись покомпонентного действия с массивом. В упоминавшейся программке вычисления спектрограммы можно две строки со стрелками заменить двумя обычными строками:

и

Значения в каждом столбце из

это

но для ICFFT нужен массив

Значения

определяются путём шаманства. В приведённой ниже программке создания wav-файла фаза вычисляется с помощью двух параметров:

задаёт долю фазы, изменяющуюся от отсчета к отсчету регулярно, а

задаёт "шум" - часть фазы, вычисляемую через псевдослучайную величину

со значениями, равномерно распределёнными от

до

При

(шума нет) картинка-спектрограмма получается неплохой, однако - лишь при согласованном выборе параметров создания wav-файла (

и вычисления спектрограммы (надо выбирать

при этом, увы, звук получается трескучий. При

(фаза содержит только шум) звук более интересный, но картинка текстурируется шумом, фотографии портятся; такой режим подходит для символических изображений.
В общем, в этом деле ещё много места для шаманства и экспериментов.

Окончание (вся программка на одном рисунке не уместилась):

В примере частота дискретизации (sample rate) аудио выбрана равной 4000 Гц. Чем она выше, тем более высокочастотный звук воспроизведётся плеером, если плеер вообще способен проигрывать аудио с частотой дискретизации, отличной от стандартной 44100 Гц, и тем меньше продлится звучание wav-файла. В данном примере, с

вот результат (ссылка на wav-файл):
https://drive.google.com/file/d/1tC719_ ... bQNi3Jjtr/Упоминавшаяся выше маткадная программка вычисления спектрограммы с параметрами


выдаёт для сигнала из этого wav-файла такую спектрограмму:

Если при синтезе wav-файла из той же исходной картинки "356x256.bmp" выбрать

то звук получается немножко страшнее (ссылка на wav-файл):
https://drive.google.com/file/d/1kY4Xoc ... UxIkduPKF/При этом и спектрограмма в Маткаде получается страшненькая:

Как видим, шум испортил фотографии; но для одних только букв или мультяшных изображений результат с шумом был бы приемлемым - они смотрелись бы всё ещё разборчиво. (В любом случае качество картинки-спектрограммы повышается при выборе хорошей исходной bmp-картинки большего размера, например,





