Ну, а что - мы ж кабаны. Давайте оценим, что он там может этот энкодер в плане точности определения скорости, как функцию координаты. Предполагаем, что устройство считывает и запоминает пары координата - время (

) на некотором отрезки, скажем 5 см. При этом точность определения координаты

Устройство считает, что на данном отрезки скорость постоянная и для каждого измерения на нем вычисляет скорость

, где

- номер измерения,

,

- координата и время, измеренные в начале отрезка. Как уже выводилось относительная погрешность такого измерения равна:

. Для упрощения оценки будем считать, что время измеряется точно, а весь вклад в погрешность дает измерения координаты. Тогда

. Пусть шаг измерения равен
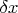
. Тогда

. Значит:

Таким образом устройство имеет набор измеренных скоростей и их погрешности -

, где

,

- скорость на отрезки. Также устройство предполагает, что скорость на этом отрезки постоянная, т.е. функция скорости от координаты

, где

- параметр этой зависимости - сама скорость на этом отрезки. Для вычисления скорости по этим данным и её погрешности устройство использует критерий

.

Матожидание

находим из условия минимума

Производная

по аргументу

в минимуме равна нулю:

Отсюда:

Погрешность

в определении скорости находим из условия:



Учитывая, что

получаем:


Решая это квадратное уравнение относительно

получим:

Окончательно получаем относительную ошибку:

Для оценки полагаем

. Тогда получаем:

Или

Полагаем устройство делает на отрезке замеры каждые 50 мкм. Тогда получается

Окончательна получаем, что относительная погрешность равна:

Тоже самое получим, если отрезок 1 см и делаем замеры каждые 10 мкм.
Ну, а если сам прибор этого не делает, то можно от него получить зависимость

и согласно этой теории рассчитать скорости с такой точностью.