Уважаемые коллеги, не знает ли кто из вас ответ на следующий вопрос (или где про это написано) ?
Пусть
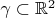
--- жорданова кривая, притом спрямляемая, и

--- её внутренняя область. На

рассмотрим такое расстояние:

--- инфимум длин ломаных, лежащих в

, с концами

и

. Верно ли, что

продолжается до непрерывной, относительно обычной евклидовой метрики, функции на

, причем при

расстояние

не превосходит длины пути с концами

и

вдоль

?
(За примерно день я так и не придумал ничего дельного.)