Всё правильно?
Не всё. Вы пользуетесь формулой типа

она даёт среднее значение физической величины, описываемой в КМ оператором

Это есть среднее значение в состоянии, описываемом волновой функцией

(Не знаю, что рассказывают в видео, потому что у меня нет и не будет времени смотреть / комментировать / рецензировать видео, но если в каком-то видео средние значения величин перепутаны с собственными значениями величин, то это никудышнее видео.)
Среднее значение величины, описываемой оператором

обычно обозначают чертой над буквой или угловыми скобками. Вот формула (с угловыми скобками) для среднего значения:

Такие интегралы Вы и вычисляли. Для среднего значения импульса ответ "ноль" - правильный. А в выражении для энергии у Вас ошибка или опечатка: постоянная Планка должна быть во второй степени.
Кстати, среднее значение энергии в стационарном состоянии (его Вы и считали) совпадает с собственным значением энергии в данном стационарном состоянии. Чтобы это увидеть, не обязательно делать такие длинные выписывания интегралов. Достаточно воспользоваться определением понятия "собственное значение энергии": по определению действие оператора энергии (он называется гамильтонианом и обозначается как

на волновую функцию стационарного состояния

сводится к умножению этой функции на собственное значение энергии

т.е. выполняется равенство

Поэтому при вычислении среднего значения мы получим под знаком интеграла выражение


это постоянная, она вынесется из под знака интеграла, а сам интеграл от

равен единице, потому что волновые функции здесь все нормированные. Таким образом:

Это верно во всех задачах с дискретным спектром собственных значений энергии, а не только в том конкретном примере, который Вы рассматриваете.
А для оператора импульса рассмотренные Вами функции

не являются собственными: оператор импульса превратил синус в косинус. Поэтому в случае с импульсом в Вашем вычислении нет речи о собственном значении импульса. Речь идёт только о среднем значении импульса.
-- 09.12.2023, 04:19 --Пока упоминавшаяся мной выше
задачка не "утонула" в форумной пучине, добавлю для нестационарного состояния

ещё пару пунктов "Найти" (возможно, такая задачка будет интересна многим начинающим изучать КМ). Итак, найти:
6) Распределение вероятности для импульса. Т.е. для упоминавшейся выше волновой функции

надо найти коэффициенты разложения по состояниям с определённым импульсом

(т.е. - по функциям

где

причём волновая функция

вне указанной в задаче потенциальной ямы равна нулю)

и изучить на графиках зависимость от импульса

квадрата модуля коэффициентов разложения. Величина

как функция переменной

имеет смысл плотности вероятности значений импульса

Это распределение вероятности относится к моменту времени

7) Распределение вероятности обнаружения частицы на том или ином уровне энергии; т.е. надо проанализировать на графике зависимость

от номера уровня

где

- коэффициенты разложения

по стационарным состояниям

см.
выше пункты (2),(4).
Вот ответы в виде графиков (при значениях параметров, указанных выше в пункте (3)):
Качественную картину распределения вероятности импульса легко предвидеть из того, что сначала волновой пакет движется со скоростью, соответствующей заданному положительному импульсу

(в этой задаче импульс мы измеряем в единицах

Поэтому в распределении вероятности значений

имеющих смысл проекций импульса на ось

должен быть "пик" при

Именно это расчёт и подтверждает: ниже на рисунках в левой части показан весь график плотности вероятности для импульса, в правой части - отдельно область графика с "пиком", чтобы была видна его ширина
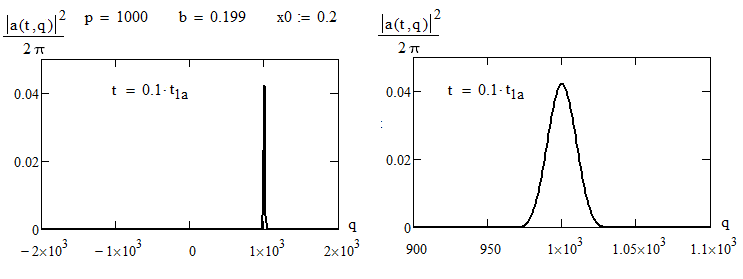
К моменту времени

центр пакета доходит до правой стенки потенциальной ямы, пакет при этом отражается назад, искажаясь по форме. Во время этого отражения пик в распределении вероятности импульса при

уменьшается, и начинает появляться другой пик - при

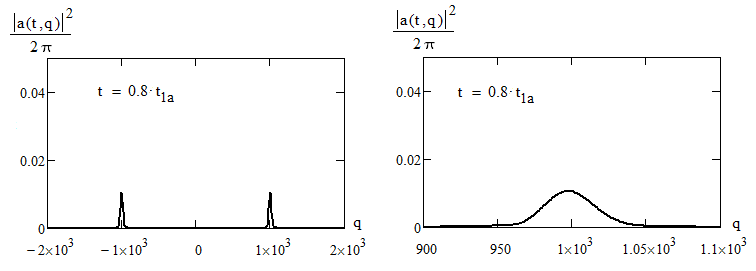
Отразившись, пакет восстанавливает свою прежнюю хорошую форму и движется в обратном направлении с импульсом, равным

При этом в распределении вероятности импульса присутствует единственный пик - при

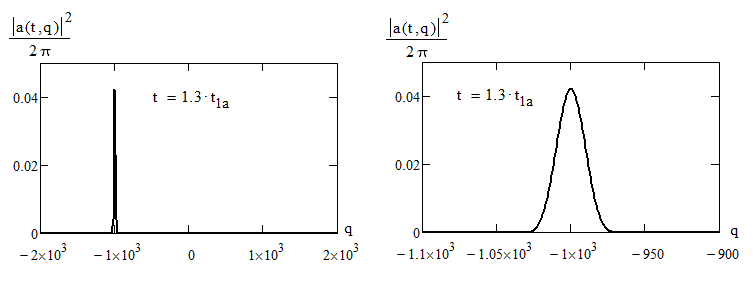
Распределение вероятности для номеров уровней энергии в данном примере имеет вид пика с центром при

(в данном примере

в единицах

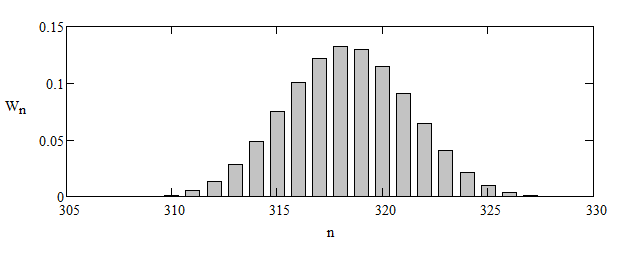
Аналогичные вычисления ещё и с другими значениями параметров помогают иллюстрировать ряд утверждений КМ:
. Соотношение неопределённости Гейзенберга для координаты и импульса: чем меньше ширина

волнового пакета по координатной оси

тем больше ширина

пика в распределении импульса, так что

(у нас

измеряется в долях от ширины ямы

импульс

измеряется в единицах
 .
. Принцип суперпозиции: волновая функция

может быть представлена линейной суперпозицией базисных функций (разложена по тому или иному функциональному базису), при этом квадраты модулей коэффициентов разложения имеют смысл распределений вероятностей в данном состоянии

(В приведённом примере требовалось найти коэффициенты

разложения

по базису, составленному из стационарных состояний в яме

а также коэффициенты

разложения по функциям
 .
. Волновая функция содержит всю доступную в КМ информацию о состоянии частицы:

- плотность вероятности для точек

в которых может обнаруживаться частица (в приведённом примере это "облако вероятности" движется и отражается от стенок ямы),

даёт распределение вероятности для значений импульса, которые могут обнаруживаться у частицы (в приведённом примере оно тоже нестационарное: положение пика периодически изменяется),

- вероятность нахождения частицы на энергетическом уровне

(эта вероятность не изменяется со временем).
Одномерное движение - дело немножко скучное. В реальном трёхмерном мире есть вращение и важна соответствующая вращениям физическая величина - момент импульса; в таких задачах будет и ещё один важный функциональный базис - "состояния с определённым моментом импульса".
. "Переходу к классическому пределу соответствуют большие квантовые числа". Вернее, почти классической картине движения частицы может соответствовать волновой пакет с достаточно большим средним по пакету импульсом

- суперпозиция стационарных состояний с большой энергией

(с большими

(Когда пакет движется быстро, его расплывание за время прохождения даже довольно большого расстояния может выглядеть незначительным.)
(P.S. Ну хорошо, больше не буду отягощать эту ветку расчётными заданиями. Наверное, топикстартеру здесь уже достаточно материала для размышлений и самостоятельных упражнений в освоении азов КМ.)