n=1 (3..2): R=5
n=2 (1..2): R=3
n=3 (7..6): R=17
n=4 (3..6): R=11
n=5 (3..5): R=7
n=6 (3..6): R=9
n=7 (8..7): R=25
n=8 (9..41): R=33
n=9 (10..41): R=43
n=10 (12..41): R=57
n=11 (9..41): R=39
n=12 (13..43): R=105
n=13 (14..44): R=135
n=14 (17..45): R=185
n=15 (13..43): R=123
n=16 (14..44): R=169
n=17 (19..45): R=219
n=18 (14..44): R=159
n=19 (26..52): R=379
n=20 (19..46): R=283
n=21 (19..52): R=377
n=22 (19..46): R=251
n=23 (14..44): R=167
n=24 (13..43): R=111
n=25 (19..46): R=297
n=26 (48..52): R=395
n=27 (19..46): R=263
n=28 (14..45): R=175
n=29 (19..46): R=233
n=30 (14..44): R=155
n=31 (12..43): R=103
n=32 (14..44): R=137
n=33 (12..42): R=91
n=34 (13..43): R=121
n=35 (14..44): R=161
n=36 (13..43): R=107
n=37 (12..41): R=71
n=38 (10..41): R=47
n=39 (8..41): R=31
n=40 (9..41): R=41
n=41 (8..41): R=27
n=42 (12..42): R=73
n=43 (12..43): R=97
n=44 (13..44): R=129
n=45 (14..45): R=171
n=46 (19..46): R=231
n=47 (19..47): R=313
n=48 (49..52): R=411
n=49 (50..52): R=543
n=50 (53..62): R=731
n=51 (49..52): R=487
n=52 (19..52): R=327
n=53 (54..62): R=859
n=54 (57..65): R=1145
n=55 (53..62): R=763
n=56 (54..65): R=1017
n=57 (58..66): R=1351
n=58 (67..66): R=1801
n=59 (57..66): R=1215
n=60 (58..66): R=1583
n=61 (54..65): R=1055
n=62 (50..62): R=703
n=63 (54..65): R=937
n=64 (57..66): R=1249
n=65 (54..65): R=871
n=66 (57..66): R=1161
n=67 (68..79): R=3097
n=68 (71..87): R=3947
n=69 (67..76): R=2631
n=70 (68..79): R=3567
n=71 (74..87): R=4763
n=72 (68..79): R=3175
n=73 (71..87): R=4233
n=74 (77..87): R=5543
n=75 (68..79): R=3695
n=76 (67..76): R=2463
n=77 (80..96): R=6569
n=78 (71..87): R=4379
n=79 (67..79): R=2919
n=80 (81..96): R=7785
n=81 (84..96): R=10087
n=82 (80..96): R=6919
n=83 (81..96): R=9225
n=84 (97..98): R=12527
n=85 (81..96): R=8351
n=86 (77..87): R=5567
n=87 (68..87): R=3711
n=88 (81..96): R=9887
n=89 (80..96): R=6591
n=90 (81..96): R=8959
n=91 (84..98): R=11945
n=92 (81..96): R=7963
n=93 (84..96): R=10415
n=94 (80..96): R=6943
n=95 (81..96): R=9257
n=96 (77..96): R=6171
n=97 (100..101): R=16457
n=98 (84..98): R=10971
n=99 (97..101): R=14695
n=100 (103..102): R=19593
n=101 (97..101): R=13255
n=102 (100..102): R=17647
n=103 (104..103): R=23529
n=104 (105..113): R=31419
n=105 (106..119): R=40959
n=106 (107..125): R=56487
n=107 (110..125): R=73063
n=108 (106..119): R=48927
n=109 (107..125): R=64255
n=110 (120..129): R=84383
n=111 (106..125): R=56255
n=112 (105..119): R=37503
n=113 (104..113): R=26623
n=114 (105..114): R=34239
n=115 (106..119): R=45127
n=116 (107..125): R=60169
n=117 (110..129): R=80225
n=118 (106..125): R=53483
n=119 (105..119): R=35655
n=120 (126..129): R=95081
n=121 (107..125): R=63387
n=122 (120..129): R=87087
n=123 (107..125): R=60975
n=124 (110..129): R=78791
n=125 (106..125): R=52527
n=126 (127..130): R=129991
n=127 (132..141): R=173321
n=128 (126..130): R=115547
n=129 (110..129): R=77031
n=130 (126..130): R=106239
n=131 (127..138): R=146599
n=132 (133..141): R=189855
n=133 (139..164): R=254911
n=134 (132..141): R=180463
n=135 (133..142): R=225023
n=136 (127..138): R=150015
n=137 (133..141): R=206847
n=138 (127..138): R=142587
n=139 (144..164): R=351359
n=140 (133..164): R=234239
n=141 (127..141): R=156159
n=142 (133..142): R=216367
n=143 (139..164): R=277615
n=144 (145..164): R=370153
n=145 (146..166): R=493537
n=146 (159..189): R=658049
n=147 (145..166): R=438699
n=148 (146..174): R=591983
n=149 (145..164): R=394655
n=150 (139..164): R=263103
n=151 (144..164): R=360361
n=152 (145..166): R=467739
n=153 (146..189): R=635519
n=154 (145..166): R=423679
n=155 (146..174): R=554143
n=156 (145..164): R=376603
n=157 (145..166): R=492571
n=158 (146..189): R=656761
n=159 (168..195): R=871915
n=160 (146..174): R=583787
n=161 (145..164): R=389191
n=162 (146..174): R=518921
n=163 (139..164): R=345947
n=164 (133..164): R=230631
n=165 (146..174): R=615017
n=166 (145..166): R=410011
n=167 (146..174): R=546681
n=168 (171..196): R=1431979
n=169 (168..195): R=970599
n=170 (168..196): R=1290267
n=171 (177..207): R=1727783
n=172 (168..196): R=1151855
n=173 (159..189): R=767903
n=174 (146..174): R=511935
n=175 (168..196): R=1365161
n=176 (168..195): R=910107
n=177 (178..208): R=2416521
n=178 (199..209): R=3216799
n=179 (177..207): R=2157291
n=180 (171..197): R=1504895
n=181 (168..195): R=1003263
n=182 (168..196): R=1302127
n=183 (171..197): R=1676703
n=184 (177..207): R=2270335
n=185 (171..197): R=1585403
n=186 (168..195): R=1056935
n=187 (159..189): R=704623
n=188 (168..195): R=939497
n=189 (146..189): R=626331
n=190 (171..197): R=1590511
n=191 (177..207): R=2120681
n=192 (168..196): R=1413787
n=193 (177..207): R=1885049
n=194 (168..196): R=1256699
n=195 (159..195): R=837799
n=196 (168..196): R=1117065
n=197 (171..197): R=1501353
n=198 (177..207): R=1993215
n=199 (212..222): R=5315241
n=200 (199..217): R=3558763
n=201 (199..222): R=4599551
n=202 (178..209): R=3066367
n=203 (199..222): R=4088489
n=204 (178..208): R=2725659
n=205 (199..222): R=3877919
n=206 (178..208): R=2585279
n=207 (171..207): R=1723519
n=208 (177..208): R=2298025
n=209 (178..209): R=3064033
n=210 (199..222): R=4063723
n=211 (199..222): R=5217727
n=212 (215..248): R=6956969
n=213 (199..222): R=4637979
n=214 (212..228): R=5978623
n=215 (220..248): R=7971497
n=216 (199..222): R=5314331
n=217 (199..217): R=3542887
n=218 (199..222): R=4723849
n=219 (212..228): R=6298465
n=220 (223..248): R=8397953
n=221 (212..222): R=5598635
n=222 (199..222): R=3732423
n=223 (230..256): R=9953129
n=224 (212..228): R=6635419
n=225 (223..256): R=8847225
n=226 (212..228): R=6355687
n=227 (223..256): R=8474249
n=228 (212..228): R=5649499
n=229 (215..248): R=7332399
n=230 (232..256): R=10011263
n=231 (212..248): R=6674175
n=232 (233..263): R=17337001
n=233 (240..263): R=22923375
n=234 (232..258): R=15410667
n=235 (233..263): R=21093689
n=236 (232..257): R=14062459
n=237 (233..263): R=18749945
n=238 (232..257): R=12499963
n=239 (232..263): R=16666617
n=240 (241..278): R=44444313
n=241 (266..278): R=56804591
n=242 (240..278): R=37869727
n=243 (241..278): R=50492969
n=244 (240..263): R=33661979
n=245 (233..263): R=22441319
n=246 (232..258): R=14960879
n=247 (230..256): R=9973919
n=248 (212..248): R=6649279
n=249 (223..256): R=8865705
n=250 (240..263): R=23456487
n=251 (232..263): R=15761255
n=252 (232..256): R=10507503
n=253 (240..263): R=28020007
n=254 (233..263): R=18901151
n=255 (232..257): R=12600767
n=256 (223..256): R=8400511
n=257 (232..257): R=11200681
n=258 (232..258): R=14934241
n=259 (233..263): R=19912321
n=260 (240..263): R=26549761
n=261 (240..263): R=35399681
n=262 (240..263): R=23599787
n=263 (232..263): R=15733191
n=264 (240..278): R=41464303
n=265 (241..278): R=55285737
n=266 (271..357): R=142886379
n=267 (266..357): R=98285755
n=268 (266..357): R=130020031
n=269 (266..357): R=87365115
n=270 (266..357): R=116486823
n=271 (281..357): R=157154471
n=272 (266..357): R=104769647
n=273 (266..357): R=69846431
n=274 (241..278): R=46564287
n=275 (266..278): R=63101607
n=276 (266..357): R=82780955
n=277 (241..278): R=55187303
n=278 (240..278): R=36791535
n=279 (266..357): R=98110761
n=280 (266..357): R=130814347
n=281 (285..358): R=174419129
n=282 (266..357): R=116279419
n=283 (271..357): R=155039225
n=284 (266..357): R=103359483
n=285 (307..362): R=275625289
n=286 (285..358): R=189535835
n=287 (266..357): R=126357223
n=288 (281..357): R=168476297
n=289 (266..357): R=112317531
n=290 (281..357): R=158560799
n=291 (266..357): R=105707199
n=292 (285..359): R=244926959
n=293 (281..357): R=163284639
n=294 (285..359): R=227588847
n=295 (271..357): R=155428635
n=296 (285..358): R=193522535
n=297 (266..357): R=129015023
n=298 (266..357): R=86010015
n=299 (285..359): R=229360041
n=300 (281..357): R=165276159
n=301 (285..358): R=203875591
n=302 (271..357): R=145324775
n=303 (266..357): R=96883183
n=304 (266..357): R=129177577
n=305 (281..358): R=172236769
n=306 (285..359): R=229649025
n=307 (308..362): R=306198703
n=308 (309..362): R=408264937
n=309 (312..362): R=544353249
n=310 (308..362): R=369953007
n=311 (309..362): R=483869551
n=312 (327..362): R=644034303
n=313 (309..362): R=430106267
n=314 (307..362): R=286737511
n=315 (308..362): R=382316681
n=316 (285..359): R=254877787
n=317 (308..362): R=339837049
n=318 (309..362): R=453116065
n=319 (312..362): R=604154753
n=320 (308..362): R=402769835
n=321 (285..359): R=268513223
n=322 (285..358): R=179008815
n=323 (309..362): R=477356841
n=324 (312..362): R=636475787
n=325 (309..362): R=424317191
n=326 (307..362): R=282878127
n=327 (328..370): R=754341673
n=328 (341..370): R=1005788897
n=329 (327..362): R=670525931
n=330 (309..362): R=447017287
n=331 (312..362): R=596023049
n=332 (308..362): R=397348699
n=333 (309..362): R=529798265
n=334 (308..362): R=353198843
n=335 (285..359): R=235465895
n=336 (271..357): R=156977263
n=337 (285..358): R=209303017
n=338 (307..362): R=279070689
n=339 (327..370): R=744188505
n=340 (328..370): R=992251339
n=341 (343..370): R=1323001785
n=342 (328..370): R=882001191
n=343 (344..378): R=2352003177
n=344 (373..394): R=3097885415
n=345 (343..378): R=2065256943
n=346 (344..394): R=2741096351
n=347 (343..378): R=1827397567
n=348 (341..370): R=1224961663
n=349 (343..375): R=1633282217
n=350 (341..370): R=1088854811
n=351 (327..370): R=725903207
n=352 (309..362): R=483935471
n=353 (308..362): R=322623647
n=354 (285..358): R=215082431
n=355 (271..357): R=143388287
n=356 (266..357): R=95592191
n=357 (266..357): R=63728127
n=358 (281..358): R=169941673
n=359 (285..359): R=226588897
n=360 (307..362): R=302118529
n=361 (308..362): R=402824705
n=362 (285..362): R=268549803
n=363 (327..370): R=716132809
n=364 (328..370): R=954843745
n=365 (341..370): R=1273124993
n=366 (328..370): R=848749995
n=367 (341..370): R=1131666663
n=368 (343..375): R=1508888879
n=369 (341..370): R=1005925919
n=370 (327..370): R=670617279
n=371 (343..378): R=1788312745
n=372 (344..378): R=2384416993
n=373 (376..394): R=3179222657
n=374 (343..378): R=2119481771
n=375 (343..375): R=1412987847
n=376 (379..394): R=3767967593
n=377 (344..378): R=2511978395
n=378 (343..378): R=1674652263
n=379 (382..394): R=4465739369
n=380 (344..394): R=2977159579
n=381 (379..394): R=3969546105
n=382 (387..425): R=10585456281
n=383 (382..425): R=7056970855
n=384 (382..425): R=9409294471
n=385 (382..425): R=6272863003
n=386 (382..425): R=8363817307
n=387 (397..425): R=11151756409
n=388 (382..425): R=7434504283
n=389 (382..425): R=4956336199
n=390 (382..425): R=6608448251
n=391 (379..394): R=4405632167
n=392 (344..394): R=2937088111
n=393 (379..394): R=3916117481
n=394 (344..394): R=2610744987
n=395 (382..425): R=6961986633
n=396 (382..425): R=9282648843
n=397 (400..456): R=24753730235
n=398 (397..455): R=16502486823
n=399 (397..456): R=22003315783
n=400 (429..456): R=28677246203
n=401 (397..456): R=19118164135
n=402 (400..456): R=25490885513
n=403 (397..455): R=16993923675
n=404 (397..425): R=11590223975
n=405 (382..425): R=7726815983
n=406 (382..425): R=5151210655
n=407 (382..425): R=6868280873
n=408 (382..408): R=4578853915
n=409 (382..425): R=6105138553
n=410 (382..425): R=8140184737
n=411 (387..425): R=10853579649
n=412 (397..455): R=14471439535
n=413 (397..456): R=19295252713
n=414 (400..456): R=25727003559
n=415 (397..455): R=17625062639
n=416 (397..425): R=11750041759
n=417 (397..455): R=15666722345
n=418 (382..425): R=10444481563
n=419 (397..455): R=13925975417
n=420 (382..425): R=9283983611
n=421 (382..425): R=6189322407
n=422 (397..455): R=16504859753
n=423 (387..425): R=11003239835
n=424 (382..425): R=7335493223
n=425 (382..425): R=4890328815
n=426 (397..445): R=13040876841
n=427 (397..455): R=17387835787
n=428 (397..456): R=23183781049
n=429 (430..456): R=30911708065
n=430 (435..458): R=41215610753
n=431 (400..456): R=27477073835
n=432 (397..456): R=18318049223
n=433 (397..433): R=12212032815
n=434 (430..458): R=32565420841
n=435 (440..458): R=43420561121
n=436 (429..456): R=28947040747
n=437 (397..456): R=19298027167
n=438 (400..456): R=25730702889
n=439 (430..458): R=34841246377
n=440 (450..458): R=45743471803
n=441 (430..456): R=30969996779
n=442 (397..456): R=20646664519
n=443 (400..456): R=27528886025
n=444 (397..456): R=18352590683
n=445 (397..445): R=12235060455
n=446 (430..458): R=32626827881
n=447 (397..456): R=21751218587
n=448 (397..455): R=14500812391
n=449 (397..456): R=19334416521
n=450 (451..458): R=50768754217
n=451 (459..458): R=67691672289
n=452 (440..458): R=45127781531
n=453 (429..456): R=30085187687
n=454 (397..456): R=20056791791
n=455 (397..455): R=13371194527
n=456 (397..456): R=17828259369
n=457 (450..458): R=47542024985
n=458 (430..458): R=31694683323
n=459 (460..461): R=84519155529
n=460 (462..461): R=112692207371
n=461 (459..461): R=75128138247
n=462 (464..471): R=200341701993
n=463 (462..463): R=133561134663
n=464 (469..491): R=346590066283
n=465 (464..491): R=237442017179
n=466 (462..466): R=158294678119
n=467 (464..491): R=211059570825
n=468 (464..491): R=281412761247
n=469 (474..491): R=349448440831
n=470 (464..491): R=250144676519
n=471 (462..471): R=166763117679
n=472 (464..491): R=222350823583
n=473 (464..491): R=292237823835
n=474 (477..491): R=383428016575
n=475 (464..491): R=263526902011
n=476 (474..491): R=351369202681
n=477 (478..496): R=468492270241
n=478 (485..497): R=575623135935
n=479 (477..491): R=416437573547
n=480 (464..491): R=277625049031
n=481 (474..491): R=370166732041
n=482 (464..491): R=254479316383
n=483 (464..491): R=329037095147
n=484 (464..491): R=219358063431
n=485 (488..497): R=584954835817
n=486 (477..491): R=402140154283
n=487 (478..496): R=519959854059
n=488 (493..500): R=683388232127
n=489 (477..496): R=455592154751
n=490 (464..491): R=303728103167
n=491 (464..491): R=202485402111
n=492 (478..496): R=539961072297
n=493 (498..500): R=719948096395
n=494 (478..496): R=486912565695
n=495 (488..497): R=639953863463
n=496 (477..496): R=426635908975
n=497 (478..497): R=568847878633
n=498 (499..500): R=758463838177
n=499 (502..506): R=1011285117569
n=500 (488..500): R=674190078379
n=501 (499..501): R=881715740415
n=502 (503..509): R=1210271371431
n=503 (504..529): R=1567494649627
n=504 (507..540): R=2089992866169
n=505 (503..509): R=1402343409087
n=506 (499..506): R=989345275647
n=507 (510..540): R=2480223622235
n=508 (504..529): R=1653482414823
n=509 (502..509): R=1122382791663
n=510 (513..541): R=2939524293019
n=511 (504..530): R=1995347185179
n=512 (510..540): R=2612910482683
n=513 (516..541): R=3483880643577
n=514 (507..540): R=2345780341887
n=515 (513..541): R=3198780775531
n=516 (524..583): R=4170276163355
n=517 (510..541): R=2780184108903
n=518 (516..541): R=3679730430703
n=519 (507..540): R=2459499360255
n=520 (513..541): R=3295033017959
n=521 (507..540): R=2196688678639
n=522 (510..541): R=2928918238185
n=523 (516..583): R=3844202252527
n=524 (534..583): R=5125603003369
n=525 (516..541): R=3499538751007
n=526 (507..540): R=2366794773743
n=527 (504..529): R=1577863182495
n=528 (507..540): R=2166507138407
n=529 (503..529): R=1444338092271
n=530 (504..530): R=1899148184679
n=531 (510..540): R=2500922855259
n=532 (513..541): R=3235193873735
n=533 (507..540): R=2156795915823
n=534 (537..583): R=5751455775529
n=535 (516..583): R=4057619222183
n=536 (510..540): R=2705079481455
n=537 (545..583): R=7025912218889
n=538 (524..583): R=4683941479259
n=539 (513..541): R=3122627652839
n=540 (504..540): R=2081751768559
n=541 (510..541): R=2775669024745
n=542 (516..542): R=3700892032993
n=543 (524..583): R=4934522710657
n=544 (537..583): R=6288557722095
n=545 (546..588): R=8772484818945
n=546 (550..589): R=10858055219359
n=547 (545..588): R=8006010325735
n=548 (546..588): R=10397019044679
n=549 (545..583): R=7116453622875
n=550 (551..590): R=17502028277929
n=551 (557..596): R=23336037703905
n=552 (550..590): R=16429857255783
n=553 (551..596): R=21529079969951
n=554 (550..590): R=14352719979967
n=555 (551..590): R=19136959973289
n=556 (550..589): R=13711348536135
n=557 (572..602): R=33020626679527
n=558 (551..596): R=22175491344543
n=559 (550..590): R=15365432803175
n=560 (546..588): R=10243621868783
n=561 (537..583): R=6829081245855
n=562 (550..590): R=16939839048319
n=563 (551..596): R=22586452064425
n=564 (550..590): R=16187451842027
n=565 (546..589): R=10791634561351
n=566 (550..589): R=13888604532735
n=567 (551..590): R=17846085581767
n=568 (557..596): R=23680967731047
n=569 (557..602): R=31726374367585
n=570 (551..596): R=21947424446791
n=571 (557..602): R=28201221660075
n=572 (592..608): R=39017643460961
n=573 (557..596): R=26011762307307
n=574 (572..602): R=34678285757567
n=575 (551..596): R=23118857171711
n=576 (550..590): R=15412571447807
n=577 (546..588): R=10275047631871
n=578 (550..589): R=13700063509161
n=579 (551..590): R=18951767785799
n=580 (550..589): R=12634511857199
n=581 (545..588): R=8423007904799
n=582 (534..583): R=5615338603199
n=583 (516..583): R=3743559068799
n=584 (546..588): R=9982824183465
n=585 (550..589): R=13310432244619
n=586 (551..590): R=17747242992825
n=587 (550..589): R=11831495328551
n=588 (545..588): R=7887663552367
n=589 (546..589): R=10516884736489
n=590 (550..590): R=14022512981985
n=591 (572..602): R=37393367951961
n=592 (603..616): R=49857823935947
n=593 (572..602): R=33238549290631
n=594 (592..608): R=43956504338111
n=595 (557..602): R=29304336225407
n=596 (551..596): R=19536224150271
n=597 (557..597): R=26262557464201
n=598 (572..602): R=35016743285601
n=599 (592..608): R=45006679419631
n=600 (557..602): R=30540204941055
n=601 (592..608): R=41501325375527
n=602 (557..602): R=27667550250351
#Дальше с пропусками
n=607 (603..621): R=58355901374591
n=608 (572..608): R=38903934249727
n=609 (603..621): R=51871912332969
n=616 (592..616): R=48575069253735
n=619 (603..621): R=56428430761599
n=621 (603..621): R=51173735510107
n=622 (603..624): R=66878140161895
n=624 (603..624): R=60650353197163



 :
:
 от
от  очень сильно похожа (
очень сильно похожа ( если отрезать начальные
если отрезать начальные  ) на прямую с коэффициентом
) на прямую с коэффициентом  или, хм, чуть меньше
или, хм, чуть меньше , дающих
, дающих  ; они, в свою очередь, зависят от
; они, в свою очередь, зависят от  (и так далее до
(и так далее до  ), и, тут, в общем, надо попроверять и попрограммировать, а если повезет, - доказать. Дерево от значений
), и, тут, в общем, надо попроверять и попрограммировать, а если повезет, - доказать. Дерево от значений  . Но сегодня наконец победил глюки с многопоточной версией (это отдельная эпопея была) и завтра она догонит текущий счёт, а там пойдёт и дальше, думаю до 100e12 или несколько дальше досчитаю.
. Но сегодня наконец победил глюки с многопоточной версией (это отдельная эпопея была) и завтра она догонит текущий счёт, а там пойдёт и дальше, думаю до 100e12 или несколько дальше досчитаю. из OEIS не воспроизвел, дошел до
из OEIS не воспроизвел, дошел до  (с пропуском
(с пропуском  , они еще где-то впереди и выбросом
, они еще где-то впереди и выбросом  ). Считаю на PARI/GP маленькими интервалами длиной
). Считаю на PARI/GP маленькими интервалами длиной  и потом совокупляю в экселе. Один такой интервал считается у меня полчаса; стыдно
и потом совокупляю в экселе. Один такой интервал считается у меня полчаса; стыдно  , которых в OEIS нет. Код:
, которых в OEIS нет. Код: строгая и простая, прямо опирается на упомянутые Вами в первом ответе соображения по модулю
строгая и простая, прямо опирается на упомянутые Вами в первом ответе соображения по модулю  . Вот, есть же какое-то
. Вот, есть же какое-то  ; если оно
; если оно  , то
, то  будет целым числом, сваливающееся в единицу за
будет целым числом, сваливающееся в единицу за  шаг, и
шаг, и  , то
, то  будет целым, и аналогично
будет целым, и аналогично  - и тоже сваливаются к единице за
- и тоже сваливаются к единице за  , чтобы получить целое
, чтобы получить целое  , а второе в
, а второе в  , что даст
, что даст  . В итоге, объединяя все три случая
. В итоге, объединяя все три случая  , получим
, получим От рекуррентности легко избавиться и записать явно
От рекуррентности легко избавиться и записать явно Оценка все еще вполне чудовищная для практического применения, например для
Оценка все еще вполне чудовищная для практического применения, например для  правая часть
правая часть  ; но уже хотя бы не настолько ужасно, как ранее найденная
; но уже хотя бы не настолько ужасно, как ранее найденная 
 . Хотя максимально обнаружен
. Хотя максимально обнаружен  около 27.67e12. Соответственно старую останавливаю, хорошо потрудилась, 107ч счёта.
около 27.67e12. Соответственно старую останавливаю, хорошо потрудилась, 107ч счёта. , а лишь добавляется одно старшее, что собственно в оценках и сделано. Но ведь бывает и сильная перестройка
, а лишь добавляется одно старшее, что собственно в оценках и сделано. Но ведь бывает и сильная перестройка  .
. второй программой. Ну или тут добавить вместо последнего print, главное не в цикл while. И это критично, например замена кода
второй программой. Ну или тут добавить вместо последнего print, главное не в цикл while. И это критично, например замена кода где
где  - константа, а
- константа, а  - ну тоже в идеале константы, или хотя бы медленно ползущие функции. Верхняя оценка уже имеет такой вид, но она грубовата:
- ну тоже в идеале константы, или хотя бы медленно ползущие функции. Верхняя оценка уже имеет такой вид, но она грубовата: 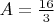 , в то время как численные наблюдения дают гораздо более скромное
, в то время как численные наблюдения дают гораздо более скромное  .
. (наименьшие
(наименьшие  по модулю
по модулю  по модулю
по модулю  ). По крайней мере это так для чисел до миллиона (и до
). По крайней мере это так для чисел до миллиона (и до  соответственно). Иное дело, что эти
соответственно). Иное дело, что эти  ; их надо поизучать дополнительно.
; их надо поизучать дополнительно. .
. . Так как
. Так как  , причём
, причём  всегда целое число (плюс возможно ещё сколько-то делений пополам, ещё больше уменьшающих
всегда целое число (плюс возможно ещё сколько-то делений пополам, ещё больше уменьшающих  , то
, то  , т.е.
, т.е.  и этот переход
и этот переход  для таких
для таких  для
для  для
для  (т.е. следующее
(т.е. следующее  для
для  выполняется 84 раза из 198 таких
выполняется 84 раза из 198 таких  для
для  .
. для
для  и это все быстро уйдет в ноль. Но для практического применения просто супер, нет смысла копаться в чересчур маленьких
и это все быстро уйдет в ноль. Но для практического применения просто супер, нет смысла копаться в чересчур маленьких  , и в целом
, и в целом  * - в смысле, она станет грубой, если избавиться от рекуррентности и написать
* - в смысле, она станет грубой, если избавиться от рекуррентности и написать  ; в терминах
; в терминах  при
при  , т.е. как часто происходит не гарантированное уменьшение следующего значения.
, т.е. как часто происходит не гарантированное уменьшение следующего значения. ).
). означает, что пока не найдены
означает, что пока не найдены 
 ; это видимо один из случаев, когда происходит "кардинальная перестройка"
; это видимо один из случаев, когда происходит "кардинальная перестройка"  (не проверял, но хочу)
(не проверял, но хочу)
 . Важно что они найдены
. Важно что они найдены  как раз найдены
как раз найдены  - n=622 (603..624) - т.е. найдено
- n=622 (603..624) - т.е. найдено  , но
, но  и
и  и все
и все  ещё остаются не найденными.
ещё остаются не найденными. - минимальное не найденное
- минимальное не найденное  - максимальное найденное. Остальное не гарантировано.
- максимальное найденное. Остальное не гарантировано. ).
).  - наименьшее
- наименьшее  , минимальный остаток по модулю 3? Т.е. наименьшее
, минимальный остаток по модулю 3? Т.е. наименьшее  ? И какое условие важнее? Как-то непонятно.
? И какое условие важнее? Как-то непонятно. - наименьшее из чисел вида
- наименьшее из чисел вида  , которому нужно
, которому нужно  с любым нижним индексом.
с любым нижним индексом. , наименьший такой:
, наименьший такой:  (последнее условие следует из
(последнее условие следует из  ), но если я правильно понимаю Ваш переход
), но если я правильно понимаю Ваш переход  , то должно быть
, то должно быть  и я даже и не знаю равно ли оно
и я даже и не знаю равно ли оно  или нет, ведь
или нет, ведь  и это всё что известно. Т.е. ни подтвердить, ни опровергнуть Ваше утверждение/предположение не могу. Возможно не вполне его понимаю.
и это всё что известно. Т.е. ни подтвердить, ни опровергнуть Ваше утверждение/предположение не могу. Возможно не вполне его понимаю. , значит Вы похоже правы.
, значит Вы похоже правы. , а первое тоже слегка перефразированное моё
, а первое тоже слегка перефразированное моё  . Т.е. это просто альтернативная формулировка.
. Т.е. это просто альтернативная формулировка. ; в противном случае к массиву
; в противном случае к массиву  просто добавляется слева единица или двойка.
просто добавляется слева единица или двойка. а именно, что не бывает
а именно, что не бывает  . Спасибо за развеивающий заблуждение пример!
. Спасибо за развеивающий заблуждение пример! , т.е. из полного разрешённого диапазона в 2/3 от предыдущего
, т.е. из полного разрешённого диапазона в 2/3 от предыдущего  как-то совсем не поровну ... Так что в каком-то смысле Вы были правы в ожиданиях.
как-то совсем не поровну ... Так что в каком-то смысле Вы были правы в ожиданиях.  .
. (если имеется в виду последний шаг перед 1) всегда
(если имеется в виду последний шаг перед 1) всегда  . Легко доказывается.
. Легко доказывается.  .
.  . Число шагов (считается только умножение на тройку) приблизительно
. Число шагов (считается только умножение на тройку) приблизительно  .
. .
. . Дальше - часы ожидания.
. Дальше - часы ожидания.