Парадокс равномерного распределения на нат. числах

[KhAl]

Doctor Boom писал(а):

Я тут кстати подумал, а как в таком случае понимать $\lim_{N \to \infty} \frac{K}{N}$, в смысле раскрытия по эпсилон-дельта формализму, ведь всегда существует вероятность при любом числе испытаний получить далекие от реальных соотношений частоты, ну например как ваше

Ну вот именно. Правда, здесь речь не о вероятности, а о возможности — Вы не ограничили рассматриваемый класс последовательностей. А что такое вероятность — надо УТОЧНЯТЬ.

Doctor Boom писал(а):

Наверное вероятность такого очень мала, но надо как-то строго показать

Нет. Сначала надо формализовать утверждение "вероятность такого очень мала". Потому что Вы начинаете с монеток — я могу, например, для конечного числа бросков монеток считать вероятности чего-либо, тут никакого Лебега не нужно. А для бесконечного числа монеток я считать вероятности не умею...

Я спрашиваю, что такое вероятность (попасть в множество), а вы начинаете загонять "вероятность мала..."

Doctor Boom писал(а):

По пределу. Если предел существует, то значит это и есть вероятность

Вы так и не сказали, предел чего и предел в каком смысле. Но хоть признали, что не понимаете, на том спасибо.

Doctor Boom писал(а):

Могу, чтобы не было слишком просто, будет работать в двоичной системе счисления, тогда так - точка точно попадает в интервал [0; 1/3], если двоичная запись имеет вид $0,00...$, вероятность этого $\frac{1}{4}$, также она точно попадает в интервал, если запись имеет вид $0,0100...$, вероятность этого $\frac{1}{16}$ и так далее, суммирует, получаем $\frac{1}{3}$

Хорошо. Это максимально не похоже на то, что Вы описали, когда я спросил, как считать вероятность. У меня была картинка в голове с последовательностями вещественных чисел, а у Вас теперь нечто совсем другое...

Так вот, Вы хотите сказать, что результат такой процедуры по определению есть мера множества? Если так сделаете, можно забыть про ту путаницу, что была до этого с пределами, но я попрошу эту процедуру строго описать: описать, какие именно величины Вы суммируете. При этом стоит до самого конца не использовать слово "вероятность", потому что как раз вероятность на отрезке [0;1] Вы и определяете. 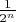Применимо к конечному числу бросков монеток (именно к буквально конечному числу бросков монеток, а не к чему-нибудь "очевидно следующему из") про вероятность говорить можно, но тоже лучше не надо, чтобы не путаться — пишите $\frac{1}{2^n}$ и всё.

То есть, что я сейчас выяснил (как мне кажется):
Вы предлагаете определять вероятность (числа попасть в множество) как сумму неких величин.

Чего я хочу:
Чтобы Вы сказали чётко и формально, что это за величины, чтобы никаких сомнений не было. Вроде "пусть задано множество $X \subset [0;1]$, по нему построим следующий набор чисел: ... (и чтобы всегда и для каждого $X$ было понятно, что это за числа), тогда вероятностью попасть в $X$ называется сумма чисел из этого набора".

На последний Ваш абзац отвечу так: сейчас интересно общее определение, а не рассчёт в частных случаях, который без общих определений может быть только взят с потолка (Вы постоянно апеллируете к понятию вероятности, которое как раз и требуется ввести). Вы везде говорите "докажем" и "следует", но определения такие, что доказывать не из чего. Например, рассуждение

Doctor Boom писал(а):

(потому что имеем стремление вероятности к нулю при последовательном прохождении по знакам)

уже требует чего-то гораздо большего, чем было сказано Вами ранее.

[mihaild]

Doctor Boom, а Вы нормальное построение тервера, в аксиоматике Колмогорова, знаете?

[Doctor Boom]

KhAl
Понятие вероятности я считаю уже известным, в частности СВ можно задать так - разбить сначала отрезок на конечное число измеримых множеств, потом для них них проделать то же самое и т.д., чтобы для каждой точки была свой уникальный адрес вида (номер первичного измеримого множества $a_i$, номер подмножества первичного измеримого множества $b_j$, номер подмножества подмножества $c_k$ и т.д.). И теперь даем распределение вероятности попадания в первичные множества, т.е. распределение на $a_i$, потом распределение для подмножеств при условии попадания в определенное первичное измеримое множество, т.е. распределение $b_j$ и т.д. Так например можно задать сингулярное распределение с функцией распределения чертовой лестницы (лестницей Кантора). Собственно так мы и задали равномерную СВ с помощью случайных цифр.
Далее нам надо найти меру какого-то подмножества $mA$ на единичном отрезке. Она по определению равна вероятности попадания в это множество равномерной СВ (по геометрическому определению вероятности), ну и далее $\lim_{N \to \infty} \frac{K}{N}$ стремится к этой вероятности по ЗБЧ

[KhAl]

Doctor Boom
Вы в каждом сообщении пишете что-то новое. Хорошо бы сброситься и попытаться понять, что вообще происходит.

Попытаюсь задать короткие и конкретные вопросы.

1. Вы пытаетесь построить нечто, "эквивалентное мере Лебега". Какие стартовые понятия Вы для этого привлекаете, что "дано"? Ответьте, не описывая свою конструкцию.

[Doctor Boom]

KhAl в сообщении #1616402 писал(а):

Вы пытаетесь построить нечто, "эквивалентное мере Лебега". Какие стартовые понятия Вы для этого привлекаете, что "дано"? Ответьте, не описывая свою конструкцию.

Понятие равновероятностного распределения на отрезке.
Вероятность попасть в множество на единичном отрезке равна мере этого множества.
ЗБЧ, при увеличении числа испытаний доля попаданий стремится к вероятности попадания, т.е. к мере

[KhAl]

Doctor Boom писал(а):

Понятие равновероятностного распределения на отрезке.

2. Приведите, пожалуйста, название учебника, из которого Вы берёте определение равновероятностного распределения, а так же место, в котором это определение находится.

[Doctor Boom]

KhAl
Ни из какого, я его задаю случайной последовательностью цифр. В более общем случае

Doctor Boom в сообщении #1616319 писал(а):

считаю уже известным, в частности СВ можно задать так - разбить сначала отрезок на конечное число измеримых множеств, потом для них них проделать то же самое и т.д., чтобы для каждой точки была свой уникальный адрес вида (номер первичного измеримого множества $a_i$, номер подмножества первичного измеримого множества $b_j$, номер подмножества подмножества $c_k$ и т.д.). И теперь даем распределение вероятности попадания в первичные множества, т.е. распределение на $a_i$, потом распределение для подмножеств при условии попадания в определенное первичное измеримое множество, т.е. распределение $b_j$ и т.д. Так например можно задать сингулярное распределение с функцией распределения чертовой лестницы (лестницей Кантора). Собственно так мы и задали равномерную СВ с помощью случайных цифр.

[KhAl]

3. Ну хорошо, задайте равновероятностное распределение "случайной последовательностью цифр". Я начну, а Вы продолжите

Равновероятностным распределением называется...

[Doctor Boom]

Случайное двоичное число вида $0,a_1 a_2 ...$ где $a_i$ СВ из множества $0$ и $1$ с равными вероятностями, задает равновероятностное распределение на отрезке

-- 07.11.2023, 00:58 --

Ну или такое распределение, при котором вероятность попадания в любую область зависит только от меры этой области. Или распределение с постоянной плотностью

[KhAl]

Doctor Boom писал(а):

Случайное двоичное число вида $0,a_1 a_2 ...$ где $a_i$ СВ из множества $0$ и $1$ с равными вероятностями, задает равновероятностное распределение на отрезке

Не понимаю это определение. Равновероятностное распределение это что? Равновероятностное распределение это и есть "случайное двоичное число"?

[Doctor Boom]

KhAl в сообщении #1616580 писал(а):

Не понимаю это определение. Равновероятностное распределение это что? Равновероятностное распределение это и есть "случайное двоичное число"?

Ну это уже юристика и игра в слова. Вы и сами можете определить, как надо

[KhAl]

Doctor Boom я вообще в первый раз про такое понятие слышу.

-- 07.11.2023, 02:51 --

Ну, я понял. Вопрос в том, верно ли, что нечто эквивалентно мере Лебега. При этом само это нечто мне предлагается определять самому, как и значение слова "эквивалентно". Так?

-- 07.11.2023, 03:05 --

Doctor Boom, вот честно, просто прочитайте какой-нибудь учебник по теории вероятностей, попутно решая задачи и советуясь здесь — как многие делают. Вам помогут. Сейчас Вы пытаетесь оперировать понятиями, определения которых не знаете, на уровне "на пальцах" (видимо, так Вас научила Википедия и некачественный научпоп), у Вас плохо получается.

Когда Вы поймёте, о каких объектах говорите, тогда поймёте, что в Ваших рассуждениях не так.

[mihaild]

mihaild в сообщении #1615817 писал(а):

Doctor Boom, а Вы нормальное построение тервера, в аксиоматике Колмогорова, знаете?

[KhAl]

(mihaild)

Ну, Вы задали очевидный вопрос...

Я просто подумал, что Doctor Boom претендует на то, чтобы обойти нормальное построение теорвера, оказалось, нет. Он хочет обойти только его изучение, при этом бросаясь словами из него же.

[Doctor Boom]

mihaild
KhAl
Хорошо, что для вас представляет такой объект

Doctor Boom в сообщении #1616579 писал(а):

Случайное двоичное число вида $0,a_1 a_2 ...$ где $a_i$ СВ из множества $0$ и $1$ с равными вероятностями

он как-то связан с равномерным распределением?

-- 07.11.2023, 03:22 --

KhAl в сообщении #1616582 писал(а):

Doctor Boom, вот честно, просто прочитайте какой-нибудь учебник по теории вероятностей, попутно решая задачи и советуясь здесь — как многие делают

Приведите такую задачу, для которой моего понимания "на пальцах" было бы недостаточно

-- 07.11.2023, 03:28 --

mihaild в сообщении #1616584 писал(а):

Doctor Boom, а Вы нормальное построение тервера, в аксиоматике Колмогорова, знаете?

Вообще любая СВ задается функцией распределения, этого пока хватало