(Оффтоп)
не думал, что более-менее освоив КМ и ОТО буду спрашивать здесь такое, но вот
Итак, если равнодействующая оказалась вне тела, то может ли она считаться полноценной равнодействующей?
Точка её приложения находится добавлением к первой силе некой вспомогательной силы

, а ко второй

. Ясно, что от выбора

будет зависеть точка приложения силы

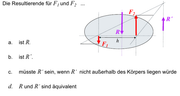
Как принято трактовать случай, если она вне тела? Т.е. на этой картинке надо выбрать между b и с(Ответ С: "должно было быть

если бы

не лежала бы вне тела"). Ссылка на рисунок кликабельна.