Вам нужно доказать ровно то утверждение, которое написано выше, а не разбирать его на части.
Нужно это утверждение для того, чтобы если потом мы сможем ещё и доказать, что Ваши два пункта выполнены, то выполнено и заключение принципа индукции.
Если Вы имеете в виду принцип индукции:

то вот доказательство:

По первому условию принципа индукции он выполняется для

. Пусть принцип индукции выполняется не для всех

, тогда найдется такое

, для которого он не выполняется. Но, поскольку для любого

существует

, а по второму условию принципа индукции имеем

, то при соблюдении этого условия не найдется такое

, для которого принцип индукции не выполняется, таким образом, он выполняется для всех
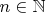
.

(Я его переделал: после Вашего замечания заменил фразу "поскольку по определению индуктивного множества для любого

существует

" -- это не верно -- на "поскольку для любого

существует

".)
О принципе индукции стоит думать как о свойстве именно

, которое можно использовать для любой формулы, а не о свойстве конкретной формулы.
Я в этом доказательстве и использую свойство

, а именно, то что каждый элемент

имеет следователя

, и каждый элемент

, кроме нуля, имеет предшественника

Есть еще доказательство (я из него взял прием от противного: "пусть не для всех

выполняется принцип индукции"), но оно основывается на принципе наименьшего числа, которое, по-моему, надо доказывать, и еще на том, что

-- это тоже надо доказывать, причем я не представляю как.
Цитата:
Предположим, что утверждение

верно не при любых

. Рассмотрим множество тех чисел, для которых оно неверно. В нем есть наименьшее число

. Это число не равно

, так как

истинно. Но тогда

истинно по выбору

. Значит, и

истинно. Пришли к противоречию.
Еще один момент. В утверждение

обязательно входит переменная, принимающая натуральные значения (иначе его нельзя было бы доказывать по индукции). Правильно?



