Ферма утверждал, что уравнение

не имеет решений в рациональных числах.
Попробуем доказать обратное.
Предположим, что такое решение существует
при

,

,

, где

,

,

- целые положительные взаимно простые числа и

, то есть

.
1.1.

, где

- целое положительное число

, где

- целое положительное число.
1.2.

,

Перемножаем левые и правые части, получаем:

,

1.3.

,

(п.1.1). Перемножаем левые и правые части, получаем:

, следовательно,

.
2.1.1 функция

в точках

и

принимает одинаковые значения разных знаков и она является целой рациональной функцией, непрерывна и определена при всех значениях

, следовательно, между

и

существует точка ( назовем ее

, значение функции в которой равно

.
2.1.3 Найдем все точки, значение функции в которых равно нулю.

.

или


,

отсюда

или

.
Поскольку

,

,

-рациональное число.
3.1.1.Найдём критические точки функции





-
точка перегиба функции.
функция

является целой рациональной функцией, непрерывна и определена при всех значениях

и ее значение равно нулю в точках 0, h и с,

,
существует три действительные точки, в которых она принимает одинаковые отрицательные значения (

,

и

) и три , в которых она принимает одинаковые положительные значения (

,

и

).

Очевидно, что может существовать два варианта расположения

относительно

- точки перегиба функции (

и

и
три варианта расположения

,

,

,

относительно друг друга:
1.

, 2.

, 3.

рассмотрим на примере варианта

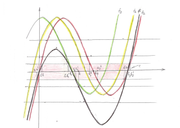
4.Выполним параллельный перенос и графика f(x) ( график на рисунке чёрной плотной линии) параллельно оси

вверх на расстояние

(удвоенное значение функции

в точке перегиба

взятое с противоположным знаком)

. Получившийся график

на рисунке обозначен жёлтым цветом.
Затем выполним параллельный перенос графика

параллельно оси

вправо на расстояние

,
так, чтобы


Получившийся график
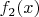
на рисунке обозначен красным цветом.

,

.

.

,

.
5.Выполним параллельный перенос графика
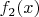
параллельно оси

влево на расстояние


Получим точки

(

,

)
и

(

,

)
6.

,


,

.

, следовательно,

Аналогично

7.

,

,

,

,

,

8.

,



,


.
аналогично

.

,

9.

,

,


10.





, следовательно

,

-рациональные числа, следовательно

,

,

,

-рациональные числа