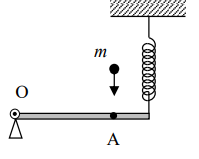
Неоднородный жесткий стержень длиной l может свободно вращаться вокруг неподвижной горизонтальной оси, проходящей через один из его концов (точку О) перпендикулярно стержню, как показано на рисунке. Другой конец стержня прикреплен к вертикальной невесомой пружине жесткостью k. В начальном равновесном состоянии стержень находится в горизонтальном положении. Линейная плотность стержня изменяется по закону

,а x – координата точки стержня, отсчитанная от точки О. В точку А на стержне (см. рис.), являющуюся его центром удара, попадает точечное тело массой m, падающее на стержень с высоты H без начальной скорости. Определите максимальную угловую скорость стержня после абсолютно неупругого соударения с телом. Сопротивлением воздуха можно пренебречь, угол отклонения стержня от горизонтали считайте малым.
Я нашел массу и момент инерции неоднородного стержня, они соответственно равны

и

. Также нашел координату центра масс стержня: 2/3l. Мои идеи по этой задаче, так как столкновение происходит в центре удара, то сохраняется импульс:

, где х - координата центра масс, энергия не сохраняется, потому что удар неупругий, также выполняется закон изменения момента импульса, но с ним у меня проблемы. Я не понимаю, как здесь его правильно записать.



