Пусть
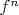
--

-ая композиционная степень отображения

,
т.е.

,

.
Сразу заметим, что

и

для любых

,

.
Допустим вопреки доказываемому, что

для некоторых

и

.
Поскольку

компактно, последовательности

и

имеют сходящиеся подпоследовательности.
Выбирая подпоследовательности этих подпоследовательностей,
получим сходящиеся последовательности

и

.
Сходящиеся последовательности фундаментальны,
а значит, найдутся

такие, что

,

.
Следовательно,



.
P.S. Непрерывность

в доказательстве не пригодилась,
да и компактность

использована не в полной мере
(например, ее можно ослабить до предкомпактности).