Две задачки по общей топологии (метрическим пространствам)

[id]

Столкнулся с двумя задачками (№297,№298* из задачника Архангельского, "Общая топология в задачах") по общей топологии:

297: Пусть $(X,p)$ - метрический компакт, а $f$ -такое отображение $X \to X$, что $p(f(x),f(y)) < p(x,y)$ для любых $x \neq y, x,y \in X$, Тогда f имеет единственную неподвижную точку.

298*. Пусть $f$ - отображение метр. компакта $(X,p)$ на себя, при котором $\forall x,y \in X: p(f(x),f(y)) \leqslant p(x,y)$. Тогда $f$ -изометрия. (т.е. $\forall x,y \in X: p(f(x),f(y)) = p(x,y)$)


Соображения по поводу первой задачи:
Рассмотрим последовательность $X_n: X_n = f(X_{n-1})$. Образ компакта - компакт, компактное подмножество хаусдорфова пространства замкнуто. Т.е. $X_n$ - центрированная система замкнутых множеств, следовательно ( по критерию компактности о непустоте пересения любой центрированной системы замк. множеств ) $Y = \bigcap\limits_{i=0}^\infty X_i \neq 0$. Видно, что $\forall x \in Y \exists y \in Y: f(y) = x$ (Прообраз $f^{-1}$ вообще может не принадлежать).
Замкнутое подмножества компакта - компакт $\Rightarrow$ $Y, Y^2$ - компакты. Сужение метрики $p$ на $Y^2$ - непрерывная функция, ограниченная и достигает максимума в точках $y_1,y_2 \in Y$. Но, как было сказано, $\exists y_1',y_2': f(y_i') = y_i$, тогда $p(y_1,y_2) < p(y_1',y_2')$, что означает противоречие если $y_1 \neq y_2$

Не уверен, правда.
По поводу второй что-то ничего путного не придумывается, а в задачнике про нее ни слова, хотя она со звездочкой даже.

Есть ли ошибки в соображениях по поводу первой? В каком направлении подумать над второй?

[redhat]

id писал(а):

Столкнулся с двумя задачками (№297,№298* из задачника Архангельского, "Общая топология в задачах") по общей топологии:

297: Пусть $(X,p)$ - метрический компакт, а $f$ -такое отображение $X \to X$, что $p(f(x),f(y)) < p(x,y)$ для любых $x \neq y, x,y \in X$, Тогда f имеет единственную неподвижную точку.

Эту задачу обсудите с Брюкволюбом -- он умный:lol:

id писал(а):

298*. Пусть $f$ - отображение метр. компакта $(X,p)$ на себя, при котором $\forall x,y \in X: p(f(x),f(y)) \leqslant p(x,y)$. Тогда $f$ -изометрия. (т.е. $\forall x,y \in X: p(f(x),f(y)) = p(x,y)$)

А вот эта задача действительно представляет интерес.

Множество $X^2=X\times X$ является компактом относительно метрики
$\rho(z_1,z_2)=p(x_1,y_1)+p(x_2,y_2)$ $z_i=(x_i,y_i)$


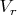
Расмотрим множество $V_r=\{(x,y)\in X^2\mid p(f(x),f(y))\le r p(x,y)\}$. Если эти множества пусты при всех $r<1$ то доказывать нечего. Предположим, что $V_R$ не пусто при некотором $0<R<1$ Ясно, что множества $V_r$ замкнуты, компактны и при $r'>r''$ имеем $V_{r''}\subseteq V_{r'}$ Введем отображение $g:X^2\to X^2$ по формуле
$g(x,y)=(f(x),f(y))$, очевидно $g(V_r)\subseteq V_r$ а следовательно $g(V_r)\subseteq V_{r^2}$


Рассмотрим множесто $W=\{(x,y)\in X^2\mid p(f(x),f(y))= p(x,y)\}$
Утв. Моножество $W$ не пусто, замкнуто компактно.
План доказательства. Пусть $(x,y)\in V_R$. Проверьте, что для любого сколь угодно близкого к 1 числа $h<1$ найдется такой номер $n$, что $(x,y)=g^n(x_n,y_n)$ и $(x_n,y_n)\in V_h$. Из последовательности $\{(x_n,y_n)\}$ можно выделить сходящуюся подпоследовательность, ее предел лежит в $W$

Утв. $g(W)\subseteq W$. -- Докажите.

Теперь самое интересное. Пусть точки $z\in V_R$ и $z'\in W$ реализуют расстояние между множествами $V_R$ и $W$. Т.е. $\min\{\rho(u,v)\mid u\in V_R,\quad v\in W\}=\rho(z,z')$
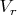
Последовательность $g^n(z),\quad n\in \mathbb{N}$ будет стремиться к неподвижной точке отображения $g$, которая лежит в пересечении всех $V_r$ при $r<R$. А итерации $g^n(z')$ будут прыгать по множеству $W$. И неравенство
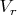
$\rho(g^n(z),g^n(z'))\le \rho(z,z')$ начиная с какого-то $n$ нарушится. Это противоресит тому, что множество $V_r$ не пусто хотябы для одного $r<1$

[id]

redhat
Так Brukvalub-то не отписался в тему, как тут обсудишь.

Теперь по поводу №298*.
$\forall 0<r<1: r > r^2 \Rightarrow V_{r^2} \subseteq V_{r}$
Как тогда получается, что если $g(V_r)\subseteq V_r$, то $g(V_r)\subseteq V_{r^2}$?

По поводу замкнутости $V_R$ - тут предлагается прости рассмотреть последовательность сходящуюся и предельным переходом в неравенстве $V_r=\{(x,y)\in X^2\mid p(f(x),f(y))\le r p(x,y)\}$ получить это же неравенство для предела?

По поводу непустоты. Тут предлагается воспользоваться предыдущей задачей, получить неподвижную точку, рассмотреть диаметр образа ( как в моем док-ве для первой) X и получить, что тогда это не будет отображением "на"? По поводу замкнутости - предельный переход в тождестве?

Цитата:

А итерации $g^n(z')$ будут прыгать по множеству $W$. И неравенство
$\rho(g^n(z),g^n(z'))\le \rho(z,z')$ начиная с какого-то $n$ нарушится.

Вот это не совсем понял.

Add:
И это

Цитата:

План доказательства. Пусть $(x,y)\in V_R$. Проверьте, что для любого сколь угодно близкого к 1 числа $h<1$ найдется такой номер $n$, что $(x,y)=g^n(x_n,y_n)$ и $(x_n,y_n)\in V_h$. Из последовательности $\{(x_n,y_n)\}$ можно выделить сходящуюся подпоследовательность, ее предел лежит в $W$

Утв. $g(W)\subseteq W$. -- Докажите.

тоже хотелось бы увидеть поподробнее.

[Brukvalub]

id в сообщении #152685 писал(а):

Так Brukvalub-то не отписался в тему, как тут обсудишь.

Не отписался, поскольку не терплю, когда "непогрешимые умники" типа redhat, не доучившие в 1-м семестре начала анализа бесконечно малых, пытаются дирижировать мной. Но потом подумал: а Вы-то чем при этом виноваты?, и решил отписаться. Мне понравилось Ваше док-во. Что именно смущает Вас в нем?

[id]

Brukvalub
Да не то чтобы смущает, просто не уверен, что оно верно, а проверить не получалось.
Спасибо за проверку.

[redhat]

id
на этом форуме не принято выкладывать полных решений, Вы меня просто закидали вопросами среди которых попадаются тривиальные. На все вопросы отвечать не буду. Додумывайте сами. Сформулируйте два главных вопроса. На них отвечу

[id]

Ну вот что касается совсем уж тривиальных, то на них я сам же и ответил.

Совсем непонятно, как у Вас получилось вот это:

Цитата:

$\forall 0<r<1: r > r^2 \Rightarrow V_{r^2} \subseteq V_{r}$
Как тогда получается, что если $g(V_r)\subseteq V_r$, то $g(V_r)\subseteq V_{r^2}$

И почему $g(V_r) \subseteq V_r$, если известно лишь что $p(f(f(x)),f(f(y))) \le p(f(x),f(y)) \le rp(x,y)$? Ведь $(f(x),f(y))$ уже не обязаны принадлежать $V_r$, если $(x,y) \in V_r$.

Ну и по мелочи -

Цитата:

А итерации $g^n(z')$ будут прыгать по множеству $W$. И неравенство
$\rho(g^n(z),g^n(z'))\le \rho(z,z')$ начиная с какого-то $n$ нарушится.

Задачка, кстати, вполне по-моему олимпиадная.

[redhat]

id писал(а):

Ну вот что касается совсем уж тривиальных, то на них я сам же и ответил.

Совсем непонятно, как у Вас получилось вот это:

Цитата:

$\forall 0<r<1: r > r^2 \Rightarrow V_{r^2} \subseteq V_{r}$
Как тогда получается, что если $g(V_r)\subseteq V_r$, то $g(V_r)\subseteq V_{r^2}$

И почему $g(V_r) \subseteq V_r$, если известно лишь что $p(f(f(x)),f(f(y))) \le p(f(x),f(y)) \le rp(x,y)$? Ведь $(f(x),f(y))$ уже не обязаны принадлежать $V_r$, если $(x,y) \in V_r$.

черт возьми! как раз это мне и казалось самым очевидным, все решения нет

[id]

redhat
Мне это сначала тоже показалось очень просто очевидным...

Надо тогда дальше подумать.

[id]

P.S. Модераторам:
Может, часть темы про вторую задачку перенести в олимпиадный раздел? Что-то тут она не решается.

[redhat]

id в сообщении #152271 писал(а):

Пусть $f$ - отображение метр. компакта $(X,p)$ на себя, при котором $\forall x,y \in X: p(f(x),f(y)) \leqslant p(x,y)$. Тогда $f$ -изометрия. (т.е. $\forall x,y \in X: p(f(x),f(y)) = p(x,y)$)

Доказательство.


$B_x(R)$ -- открытый шар в $X$ с центром в $x$ радиуса $R$.

Лемма. Для любого $x\in X$ и любого $w\in f^{-1}(x)$ будет $B_w(R)\subseteq f^{-1}(B_x(R))$.

Док-во. Пусть $z\in B_\xi(R)$ т е $p(z,\xi)<R,\quad f(\xi)=x$
Надо показать, что $\eta=f(z)\in B_x(R)$. Имеем $p(\eta,x)=p(f(z),f(\xi))\le p(z,\xi)<R$


Пусть теперь $X^2=X\times X$ и $g=f\times f$ и
$B^2_{(u,v)}(R)=B_u(R)\times B_v(R).$

Лемма. (Типа теоремы Пуанкаре о возвращении) Для любого $z=(x,y)\in X^2$ существует последовательность
$z_k\to z$ и $\{m_k\}\subseteq \mathbb{N}$ такие, что $z_k\in g^{-m_k}(z)$.

Док-во. Покажем, что для любого $\varepsilon>0$
найдется $n\in \mathbb{N}$
такое, что $g^{-n}(B^2_z(\varepsilon))\bigcap B^2_z(\varepsilon)\ne\emptyset$
В силу предыдущей леммы и компактности $X^2$ (а именно в силу того, что для любого $\varepsilon>0$ вский компакт допускает конечную $\varepsilon-$сеть) найдется $n,j$
такие, что $ g^{-n-j}(B^2_z(\varepsilon))\bigcap g^{-j}(B^2_z(\varepsilon))\ne\emptyset$, отсюда получаем требуемое.

Предроложим, что для некоторой пары точек $(x,y)\in X^2$ будет $p(f(x),f(y))<p(x,y)$.
По лемме $x_k\to x$ $y_k\to y$ и $f^{m_k}(x_k)=x$ $f^{m_k}(y_k)=y$. При достаточно больших $k$ будет
$p(f(x_k),f(y_k))\le cp(x,y)$ при некотором $c<1$

Имеем $p(x,y)=p(f^{m_k}(x_k),f^{m_k}(y_k))\le p(f(x_k),f(y_k))\le cp(x,y)$
Противоречие

id в сообщении #152271 писал(а):

Но, как было сказано, $\exists y_1',y_2': f(y_i') = y_i$, тогда $p(y_1,y_2) < p(y_1',y_2')$, что означает противоречие если $y_1 \neq y_2$

не пониаю, а как получить противоречие если окажется, что $y_1=y_2$ и $y_1'=y_2'$?
Может Брюкволлюб на этот вопро ответит раз

Brukvalub в сообщении #152687 писал(а):

Мне понравилось Ваше док-во.

[redhat]

Прошу прощения за оффтоп.

Brukvalub
В другой ветке topic16887.html
осталась проблема с Вашим высказыванием, прокомментируйте пожалуйста.

PAV:

Перенесено из посторонней темы

[Brukvalub]

redhat в сообщении #153388 писал(а):

Brukvalub
В другой ветке http://dxdy.ru/topic16887.html
осталась проблема с Вашим высказыванием, прокомментируйте пожалуйста.

Сначала научитесь уважать людей и не коверкать их ники, а потом требуйте ответов.
Кроме того, ответ там очевиден - попробуйте сами пораскинуть мозгами на тему: "Что есть док-во "от противного"".
Если не получится, то я подключусь и разъясню.

[redhat]

Brukvalub писал(а):

redhat в сообщении #153388 писал(а):

Brukvalub
В другой ветке http://dxdy.ru/topic16887.html
осталась проблема с Вашим высказыванием, прокомментируйте пожалуйста.

Сначала научитесь уважать людей и не коверкать их ники, а потом требуйте ответов.
Кроме того, ответ там очевиден - попробуйте сами пораскинуть мозгами на тему: "Что есть док-во "от противного"".
Если не получится, то я подключусь и разъясню.

Это была тривиальная задачка из Комогорова Фомина, я знал, что Вы ее не решите, дальше 1-2 курса матана Ваша деятельность не простирается.

[Brukvalub]

См.http://dxdy.ru/topic16993.html