Так как

- точка перегиба,

и

симметричны относительно точки перегиба
А почему они должны быть симметричны относительно точки перегиба?
Я тоже сейчас об этом подумала...
У меня вообще не стыкуется некоторые вещи:
Критические точки ведь идут одна за 2? А при нечётных показателях должно быть нечётное количество действительных корней уравнения.
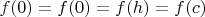
- Это получается 4 корня, если

критическая точка? Что с этим делать? Какой вывод?
И с проверкой на перегиб тоже непонятно. Я вроде как радоваться должна, что у меня выходит что при


- не критическая точка. Но ведь при чётных степенях она железно критическая точка. Где у меня ошибка?