Орбиты планет звездной системы.
На примере Солнечной системы рассмотрим характеристики движения планет вокруг звезды (Солнца).
Исходные предположения.1. В виду больших расстояний размеры планет игнорируем и рассматриваем их, как точки в пространстве.
2. Всю массу звезды (Солнца) поместим в точку, вокруг которой вращаются планеты.
Пусть

- масса данной планеты,

- масса звезды (Солнца).
Закон всемирного тяготения выполняется,

Но по второму закону Ньютона

.
Тогда

и следовательно

.

- это ускорение, которое приобретает планета под воздействием звезды. Это нормальное ускорение и направлено оно к звезде.
Чтобы планета не сближалась со звездой, она должна иметь определенную скорость движения по круговой орбите вокруг звезды.

подставим это выражение вместо ускорения.

отсюда

,
где

- гравитационная постоянная, а

- масса звезды.
Так как масса звезды не меняется, то для всех планет выполняется

, где

А если вспомнить, что

, где

- период обращения планеты, то

Следовательно, для всех планет, двигающихся по орбитам вокруг звезды, выполняется следующее

, где
 Следствие
Следствие: зная характеристики движения планеты по орбите можно узнать массу звезды.
Орбиты планет вокруг звезды представляют из себя элипсы, а расчет велся для круговых орбит.
Формула элипса с началом координат в фокусе имеет вид

,

- эксцентриситет,

- константа
Если угол

, то

.
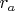
- афелий (максимальное удаление от звезды).
Если угол

то

.

- перигелий (максимальное сближение со звездой).

,

следовательно

или

или


- характеристика элиптической орбиты, это константа. Ее и будем брать, как эквивалентный радиус круговой орбиты.
Проверка соответсвия реальных данных для планет Солнечной системы и теоретических умозаключений.


- масса Солнца,
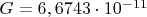

- гравитационная постоянная,



Расчет для Земли.
Данные брались из Википедии.






сут





Для Меркурия


Для Венеры


Для Марса


Для Юпитера


Для Сатурна


Для Урана


Для Нептуна


Результат для Меркурия так отличается от других планет возможно потому, что для него Солнце уже выступает не как точечный объект с массой.
На значения Марса и Сатурна возможно имеет влияние Юпитер, как самая массивная планета.



