Попытка доказательства теоремы ферма 3

[natalya_1]

Onoochin в сообщении #1600043 писал(а):

natalya_1 в сообщении #1600036 писал(а):

$a+b'=c$

Это условие откуда появилось? До этого оно отсутствовало

Из симметрии графиков f(x) и f_2(x): $a+b'=c$, $b+a'=c$, $a_1+b_2'=c$, $a_1'+b_2=c$,

Из симметрии графиков f(x) и f_3(x): $b_1'+a_2''=2h+3(k-h)$,
$b_1'+a_2'=2h$, $b_1+a_2'=2h$

[Onoochin]

natalya_1 в сообщении #1600045 писал(а):

Из симметрии графиков f(x) и f_2(x): $a+b'=c$, $b+a'=c$, $a_1+b_2'=c$, $a_1'+b_2=c$,

Многочлен для $a$
$(cd-p)x^3-c^{2}dx^2+c^{2}px=0$
Многочлен для $b'$
$(cd-p)x^3-c(2cd-3p)x^2+c^{2}(cd-p)px=0$

Какая между этими графиками симметрия?

[natalya_1]

Onoochin в сообщении #1600046 писал(а):

natalya_1 в сообщении #1600045 писал(а):

Из симметрии графиков f(x) и f_2(x): $a+b'=c$, $b+a'=c$, $a_1+b_2'=c$, $a_1'+b_2=c$,

Многочлен для $a$
$(cd-p)x^3-c^{2}dx^2+c^{2}px=0$
Многочлен для $b'$
$(cd-p)x^3-c(2cd-3p)x^2+c^{2}(cd-p)px=0$

Какая между этими графиками симметрия?

$\frac{c}{2}-b'=a-\frac{c}{2}$
$\frac{c}{2}-a_1=b_2'-\frac{c}{2}$, $h_1-\frac{c}{2}=\frac{c}{2}-h$ итд

[Onoochin]

natalya_1 в сообщении #1600047 писал(а):

$\frac{c}{2}-b'=a-\frac{c}{2}$
$\frac{c}{2}-a_1=b_2'-\frac{c}{2}$, $h_1-\frac{c}{2}=\frac{c}{2}-h$ итд

Действительно, замена $x'=c-x$ переводит многочлен $F(x)=(cd-p)x^3-c^{2}dx^2+c^{2}px$
в $F(x')=-f(x)=-\left[(cd-p)x^3-c(2cd-3p)x^2+c^{2}(cd-p)px\right]$.

По крайней мере это сильно упрощает задачу. Теперь можно избавиться от штрихованных чисел через $a'_i=c- b_i$, $b'_i=c-a_i$.

Перепишем в п. 4.1.2

Цитата:

$b-b'=d\,\,\to\,\,b-c+a=d$

что верно

Цитата:

$b_1+a_2=2h-(a_2'-a_2)$,

$b_1=2h-c+b_2$ - почему так, просьба объяснить

Цитата:

$b_2+a_1=c-(b_2'-b_2)$

$a_1=c-(c-a_2)\,\,\to\,\, a_1=a_2$ ???

[natalya_1]

Onoochin в сообщении #1600131 писал(а):

$b_1=2h-c+b_2$ - почему так, просьба объяснить

Я не поняла, откуда вы взяли это равенство. оно не верно.
Из $b_1+a_2=2h-(a_2'-a_2)$ следует $b_1=2h-(a_2+a_2'-a_2)=2h-a_2'$

-- Чт июл 06, 2023 22:22:31 --

Onoochin в сообщении #1600131 писал(а):

Цитата:

$b_2+a_1=c-(b_2'-b_2)$

$a_1=c-(c-a_2)\,\,\to\,\, a_1=a_2$ ???

Здесь у вас тоже ошибка: Из $b_2+a_1=c-(b_2'-b_2)$ следует
$a_1=c-b_2'=c-(c-a_1)$

[Onoochin]

natalya_1 в сообщении #1600133 писал(а):

Здесь у вас тоже ошибка: Из $b_2+a_1=c-(b_2'-b_2)$ следует
$a_1=c-b_2'=c-(c-a_1)$

Это не ошибка, это потому что Вы не определили Ваши штрихованные переменные. Есть два варианта переписи этих переменных
$a'_1=c-b_1$, $a'_1=c-b_2$
Какой из них правильный?
Либо перепишите эти равенства через нештрихованные переменные сами.

Ваше движение графиков свелось к введению штрихованных переменных и еще одного корня $h_1=c-h$ (из-за симметрии многочленов). К решению задачи это никак не приблизило. Как у Вас было единственное равенство
$a+a_1+a_2=b+b_1+b_2=0+h+c$
так оно и осталось.

[natalya_1]

Onoochin в сообщении #1600151 писал(а):

natalya_1 в сообщении #1600133 писал(а):

Здесь у вас тоже ошибка: Из $b_2+a_1=c-(b_2'-b_2)$ следует
$a_1=c-b_2'=c-(c-a_1)$

Это не ошибка, это потому что Вы не определили Ваши штрихованные переменные. Есть два варианта переписи этих переменных
$a'_1=c-b_1$, $a'_1=c-b_2$
Какой из них правильный?

Я всё определила (даже картинку для наглядности прикрепила), и вариант только один :
$a_1'+b_2=c$, $a_1'=c-b_2$,
$a_2'+b_1=2h$, $a_2'=2h-b_1$

-- Пт июл 07, 2023 00:29:22 --

Onoochin в сообщении #1600151 писал(а):

Ваше движение графиков свелось к введению штрихованных переменных и еще одного корня $h_1=c-h$ (из-за симметрии многочленов). К решению задачи это никак не приблизило. Как у Вас было единственное равенство
$a+a_1+a_2=b+b_1+b_2=0+h+c$
так оно и осталось.

Неправда.
Равенство у меня не единственное:
$a+a_1+a_2=a'+a_1'+a_2''-3(k-h)=0+h_1+c-3(k-h)$, $a_2''-a_2=3(k-h)$
$b'+b_1''+b_2'=0+h_1+c=b+b_1+b_2+3(k-h)$, $b_1''=b_1+3(k-h)$

Отсюда

$(b-b')-[(b_1'-b_1)+(b_2'-b_2)]=0$
$(a'-a)-[(a_1-a_1')+(a_2-a_2')]=0$
-- Пт июл 07, 2023 00:45:55 --

Onoochin в сообщении #1600151 писал(а):

Ваши штрихованные переменные.

У меня здесь нет переменных. не штрихованных, не нештрихованных.
Это всё числа

[natalya_1]

natalya_1 в сообщении #1600157 писал(а):

Я всё определила (даже картинку для наглядности прикрепила), и вариант только один :
$a_1'+b_2=c$, $a_1'=c-b_2$,
$a_2'+b_1=2h$, $a_2'=2h-b_1$


$(b-b')-[(b_1'-b_1)+(b_2'-b_2)]=0$
$(a'-a)-[(a_1-a_1')+(a_2-a_2')]=0$

И это даёт мне возможность прийти к

natalya_1 в сообщении #1599749 писал(а):

$b_1+a_2=2h-(a_2'-a_2)$,
$b_2+a_1=c-(b_2'-b_2)$;
$a+b=c+(a-a')=c+d$
$(a_2'-a_2)+(b_2'-b_2)=d$.

Далее

$b_2'-b_1'=b_2'-(b_1''-3(k-h))=(a_2'-a_1')+3(k-h)$,
$b_2'-b_1'=(c-a_1)-(2h-a_2)=(a_2-a_1)+(c-2h)=(a_2-a_1)+3(k-h)=b_2-b_1$,
$(b_2'-b_2)=(b_1'-b_1)=\frac{d}{2}$.
Отсюда
4.1.3. $a_1+b_2=c-\frac{d}{2}$- рациональное число,
$a_2+b_1=2h-\frac{d}{2}$- рациональное число.

Вы занимаетесь преобразованием многочлена, из-за этого у вас получается свистопляска с переменными. А у меня нет переменных.

-- Пт июл 07, 2023 03:00:26 --

Onoochin в сообщении #1600131 писал(а):

Теперь можно избавиться от штрихованных чисел

Нельзя от них избавляться, это конкретные числа

[Antoshka]

Onoochin в сообщении #1600131 писал(а):

Теперь можно избавиться от штрихованных чисел через $a'_i=c- b_i$, $b'_i=c-a_i$.

natalya_1 хочет сказать, что от штрихованных переменных нельзя избавляться, потому что это конкретные числа. Под конкретными числами понимаются в данном случае три, пять, семнадцать и так далее. Вот представьте, что на месте этих переменных стоят три, пять, семнадцать. Вот потому их трогать и нельзя. Десять лет назад возникали подобные непонятки, поэтому я пояснил ещё конкретнее, что имеет ввиду natalya_1

[natalya_1]

Antoshka, спасибо за разъяснения.

Промежуточный итог: ошибка в моём "доказательстве" пока не найдена.

[Onoochin]

natalya_1 в сообщении #1600157 писал(а):

У меня здесь нет переменных. не штрихованных, не нештрихованных.
Это всё числа

А буковка $x$ в

Цитата:

2.1.1 функция $y=(cd-p)x^3-c^{2}dx^2+c^{2}px$ в точках $a$ и $b$ принимает одинаковые значения разных знаков и она является целой рациональной функцией, непрерывна и определена при всех значениях $x$,

- она для новой постоянной? И каково ее значение?

А что переменные или числа, это всё равно. Между штрихованными и нештрихованными имеется простая связь $a'_i=c-b_j$, $b'_j=c-a_i$, $i,j=1,2$. Наличие этой связи позволяет исключить штрихованные "числа".

natalya_1 в сообщении #1600157 писал(а):

Я всё определила (даже картинку для наглядности прикрепила), и вариант только один :
$a_1'+b_2=c$, $a_1'=c-b_2$,
$a_2'+b_1=2h$, $a_2'=2h-b_1$

Если $a_1'=c-b_2$, то из симметрии многочленов $b_1=c-a'_2$. Отсюда получаем
$a_2'=2h-b_1\,\,\to\,\, a'_2=2h-(c-a'_2)\,\,\to\,\, 2h=c$
Как это понимать?

[natalya_1]

Onoochin в сообщении #1600299 писал(а):

natalya_1 в сообщении #1600157 писал(а):

У меня здесь нет переменных. не штрихованных, не нештрихованных.
Это всё числа

А буковка $x$ в

Цитата:

2.1.1 функция $y=(cd-p)x^3-c^{2}dx^2+c^{2}px$ в точках $a$ и $b$ принимает одинаковые значения разных знаков и она является целой рациональной функцией, непрерывна и определена при всех значениях $x$,

- она для новой постоянной? И каково ее значение?

Конечно, на кривой графика множество точек. Из всего этого бесконечного множества мы выделили те которые отвечают нашей системе равенств
$a^3+b^3=c^3$, $a^2+b^2=c^2+p$ $a+b=c+d$. B точках $a$ и $b$ она принимает одинаковое значение разных знаков

-- Пт июл 07, 2023 20:04:59 --

Onoochin в сообщении #1600299 писал(а):

natalya_1 в сообщении #1600157 писал(а):

А что переменные или числа, это всё равно. Между штрихованными и нештрихованными имеется простая связь $a'_i=c-b_j$, $b'_j=c-a_i$, $i,j=1,2$. Наличие этой связи позволяет исключить штрихованные "числа".

Нет, потому что между ними существует не простая, а попарная связь.

-- Пт июл 07, 2023 20:10:17 --

Onoochin в сообщении #1600299 писал(а):

natalya_1 в сообщении #1600157 писал(а):

natalya_1 в сообщении #1600157 писал(а):

Я всё определила (даже картинку для наглядности прикрепила), и вариант только один :
$a_1'+b_2=c$, $a_1'=c-b_2$,
$a_2'+b_1=2h$, $a_2'=2h-b_1$

Если $a_1'=c-b_2$, то из симметрии многочленов $b_1=c-a'_2$. Отсюда получаем
$a_2'=2h-b_1\,\,\to\,\, a'_2=2h-(c-a'_2)\,\,\to\,\, 2h=c$
Как это понимать?

Так и понимать: Симметрия попарная, $a_2'$ и $b_1$ не симметричны относительно $\frac{c}{2}$.
$a_2''$ и $b_1$ симметричны относительно $\frac{c}{2}$.

Будет вот так: $a_2'=2h-b_1\,\,\to\,\, a'_2=2h-(c-a''_2)\,\,\to\,\, 2h=c-(c-b_1)+a_2'=b_1+a_2'$

[Onoochin]

natalya_1 в сообщении #1600301 писал(а):

Так и понимать: Симметрия попарная, $a_2'$ и $b_1$ не симметричны относительно $\frac{c}{2}$.
$a_2''$ и $b_1$ симметричны относительно $\frac{c}{2}$.

Насчет рисования графиков ничего сказать не могу. Но из многочленов (приведены выше и которые получены из Ваших формул) либо $a'_2=c-b_1$, либо $a'_1=c-b_1$.
Вы как-нибудь определитесь и дайте однозначный ответ

Или мы вернемся назад и будем разбирать, как получен второй многочлен?

[natalya_1]

Onoochin в сообщении #1600315 писал(а):

natalya_1 в сообщении #1600301 писал(а):

Так и понимать: Симметрия попарная, $a_2'$ и $b_1$ не симметричны относительно $\frac{c}{2}$.
$a_2''$ и $b_1$ симметричны относительно $\frac{c}{2}$.

Насчет рисования графиков ничего сказать не могу. Но из многочленов (приведены выше и которые получены из Ваших формул) либо $a'_2=c-b_1$, либо $a'_1=c-b_1$.
Вы как-нибудь определитесь и дайте однозначный ответ

Или мы вернемся назад и будем разбирать, как получен второй многочлен?

Ни то, ни другое.
Я никакие многочлены не выводила. И ваши выводы получены не из моих формул.
Я давно определилась и все формулы выписала:
$a_2'=2h-b_1$, $a_2''=c-b_1$, $a_1'=c-b_2$
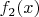
Точка $a_2'$ не принадлежит графику функции $f_2(x)$ и никаким боком не участвует в вашей связке многочленов, она принадлежит графику функции $f_3(x)$ . И у неё другой многочлен и другая связь через симметрию $b_1$ и $a_2'$ относительно $h$, а не относительно $\frac{c}{2}$

Я вообще не понимаю, почему нельзя просто проверить то, что я написала. Зачем городить дополнительный огород и всё запутывать?

[Onoochin]

Имеем два многочлена $f(x) =(cd-p)x^3-c^{2}dx^2+c^{2}px=0$.
и $f_2(x)=f_1(x-(k-h))=f(x+h-k)-2f(k)=-f(c-x)$, "антисимметричных" друг другу.

Цитата:

Из симметрии графиков f(x) и f_2(x): $a+b'=c$, $b+a'=c$, $a_1+b_2'=c$, $a_1'+b_2=c$,

Если $a+b'=c$ и $a_1+b_2'=c$, то между корнями $a,a_1,a_2$ ур-ния $f(x)=A$ где А - некоторое число, и корнями $b',b_1',b_2'$ ур-ния $f_2(x)=-A$ имеется прямая связь, что подтверждается
$f_2(x')=-A\,\,\to\,\,-f(c-x')=-A$ или для корней $b'$ $f(c-b')=A\,\,\to\,\,f(a)=A$ - что соответствует исходному ур-нию.

Совершенно аналогично получаем связь между корнями $b,b_1,b_2$ ур-ния $f(x)=-A$ и корнями $a',a_1',a_2'$ ур-ния $f_2(x)=A$

Поэтому либо $a'_2=c-b_1$, либо $a'_1=c-b_1$.

Отсюда остается вопрос: каким образом было получено, что $2h=c$ ?