Хотя давление ЭМ-волны легко получить из закона сохранения импульса системы "поле плюс заряды", любителям покопаться в микроскопическом происхождении подобных сил покажу простенький расчет в геометрии нормального падения, когда-то выложенный на форуме Мембраны и давно сгинувший вместе с сайтом. Используется система единиц Хевисайда (без лишних

в плотности энергии и т.п.). Суть расчета такова - электрическое поле

в среде вызывает электрический ток

, параллельный полю, и на этот ток действует магнитное поле волны

, создавая силу вдоль нормали (силу давления).
Итак, пусть на плоскую поверхность тела (

) из вакуума (

) перпендикулярно падает вдоль оси

плоская ЭМ волна с линейной поляризацией электрического поля вдоль оси

и магнитного поля вдоль оси

:

,

[при

]. Здесь

и

- вещественные параметры. В силу уравнений Максвелла

и

.
(Комплексная форма полей и токов выбрана здесь чисто для удобства дифференцирования - чтобы не писать уйму синусов и косинусов. Можно считать, что в получаемых выражениях физсмысл имеет только реальная часть. Либо, что удобней - что билинейные комбинации вроде вектора Пойнтинга вычисляются не как

, а как

, где

означает комплексное сопряжение.)
Пусть эта волна порождает в области вакуума

отраженную волну

,

,
где

- комплексная амплитуда отражения. Знак минус в выражении для магнитного поля диктуется уравнениями Максвелла и связан с противоположным направлением волнового вектора.
Пусть во внутренней области тела

возникает волна, проходящая вглубь и затухающая там:

,

.
Здесь

- комплексная константа с

(затухание, хотя бы слабое!), зависящая от материала тела (точнее - от микроскопических токов в нем, от проводимости). Так как на границе тела тангенциальные компоненты

и

непрерывны, то

и

.
Величину тока в системе можно определить из уравнений Максвелла
[

,

в СГС].
Записывая

[в предположении линейной связи между

и

и одинаковой зависимости их фаз от

и

], имеем:

,

,
откуда

и

.
Таким образом, все поля и токи в системе оказываются выраженными через два вещественных

и один комплексный
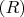
параметр. Для затухающей волны

амплитуда отражения

обязана иметь неисчезающую мнимую часть.
Теперь все готово для вычисления сил и импульсов. Следующие шаги (через вектор Пойнтинга) описаны не вполне строго, но их легко обосновать, рассматривая волновые пакеты, составленные из описанных выше плоских волн, и отбрасывая в интегралах быстро осциллирующие члены.
Вектор Пойнтинга дает плотность импульса

падающей волны:

.
Для отраженной волны

.
За большое время

со стороны падающей и отраженной волны телу передается импульс

[здесь

- поперечный размер тела, а фактор

связан с объемом области, занятой волной]. Волна, проникающая в тело, затухает и потому ограничена по своей протяженности. Поэтому ее импульс (пропорциональный объему) не содержит большого фактора

, и он может быть отброшен при рассмотрении баланса импульсов и сил. Соответственно давление света, найденное через вектор Пойнтинга, равняется

.
То же самое давление можно найти микроскопически через силу, действующую со стороны волны на ток. Объемная плотность силы равна

, а давление есть интеграл от плотности по

:
![$p = \int[(1/c) \operatorname{Re}(J_x H_y^\dag)]dz = \operatorname{Re}(JH'^\dag)/(2c \operatorname{Im} k')$ $p = \int[(1/c) \operatorname{Re}(J_x H_y^\dag)]dz = \operatorname{Re}(JH'^\dag)/(2c \operatorname{Im} k')$](https://dxdy-04.korotkov.co.uk/f/7/c/8/7c8f41620e93b19ffd4127cce88995a982.png)
или
![$p = E^2 \operatorname{Im}[-2R (1-R^\dag)/(1+R)] / \operatorname{Im}[(1-R)/(1+R)]$ $p = E^2 \operatorname{Im}[-2R (1-R^\dag)/(1+R)] / \operatorname{Im}[(1-R)/(1+R)]$](https://dxdy-02.korotkov.co.uk/f/5/8/2/582c01566ddadf5696c479963981c42982.png)
.
Так как
![$\operatorname{Im}[(1-R)/(1+R)] = -2 \operatorname{Im}R/|1+R|^2$ $\operatorname{Im}[(1-R)/(1+R)] = -2 \operatorname{Im}R/|1+R|^2$](https://dxdy-01.korotkov.co.uk/f/c/3/5/c35c5298923dfb2808b6865770cdc17582.png)
и
![$\operatorname{Im}[R (1-R^\dag)/(1+R)] = \operatorname{Im} R (1+|R|^2)/|1+R|^2$ $\operatorname{Im}[R (1-R^\dag)/(1+R)] = \operatorname{Im} R (1+|R|^2)/|1+R|^2$](https://dxdy-04.korotkov.co.uk/f/b/5/7/b57d25628646a2d88f4ce962ba481d7282.png)
,
то это выражение действительно дает

.
Так что давление света можно считать любым способом - хоть через вектор Пойнтинга, хоть через силу Ампера. Ответ одинаков. В случае полного отражения

давление вдвое больше, чем в случае полного поглощения

при той же плотности энергии падающей волны.
Отметим, что плотность энергии падающей волны равна

,
а плотность энергии отраженной волны равна

.
Видно, что давление света равно сумме этих двух плотностей:

,
что в точности соответствует давлению, оказываемому потоком безмассовых частиц, которые движутся со скоростью

и частично упруго отражаются назад от поверхности.



