Повторю картинку из первого поста, скриншот с видео:
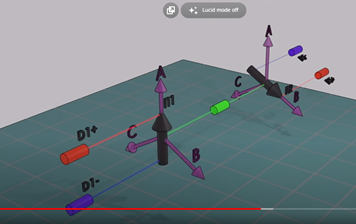
Тут есть три возможных вектора A, B и C, на которые устанавливается прибор Штерна-Герлаха, под углами 120 градусов.
Далее я вставлю в пост текст с Луркоморья, надеюсь я не нарушаю какие-то правила, прошу прощения если что:
(Оффтоп)
Цитата:
Допустим, что дано множество некоторых объектов. Например, девиц в Петушках. Как известно, после того как корабли седьмого американского флота покинули станцию Петушки, там образовались три подмножества девиц: блондинки, партийные и изнасилованные. Назовем их A, B и C. В общем случае эти множества могут пересекаться, а могут и не пересекаться. То есть может оказаться так, что среди изнасилованных нет ни одной беспартийной. Чтобы не заморачиваться, будем считать, что все множества пересекаются, но пересечение может оказаться пустым. Также для простоты будем считать, что все, кто не блондинки — брюнетки. Множества брюнеток, беспартийных и нетронутых назовем ~A, ~B и ~C.
Парадокс в том, что, казалось бы, закрепив дальнодействие как факт, Неравенство Белла тем самым казалось бы дискредитировало теорию относительности с её строгим близкодействием. Но ввиду того, что корреляции спутанных частиц носят строго вероятностный характер, становится невозможно передать осмысленное действие куда-либо мгновенно, или (что является прямым выводом ТО) в собственное прошлое, например застрелить собственного дедушку до того, как он успешно оплодотворил твою бабушку, создав тем самым причинно-следственный парадокс. Собственно в ТО сверхсветовая передача сигнала и запрещалась прежде всего именно из-за потенциала создать такие парадоксы. Но КМ почти парадоксальным образом, нарушая постулат, тем не менее соблюла основной момент: ненарушение принципа причинности. В итоге и овцы оказались целы, и волки сыты, а квантмех в очередной раз продемонстрировал своё умение сидеть сразу на двух стульях, словно так и надо.
Суть неравенства Белла такова: при любом количестве блондинок и брюнеток, партийных и беспартийных, изнасилованных и нетронутых, соблюдается такое неравенство: //, что в переводе на русский язык означает, что количество беспартийных блондинок (неважно, изнасилованных или нетронутых), то есть N(A,~B) плюс количество партийных, но нетронутых (неважно, блондинок или брюнеток), то есть N(B,~C) больше либо равно количеству нетронутых блондинок, то есть N(A,~C).
Доказательство проще шпареной попы (см. пруфпик). Количество беспартийных блондинок равно количеству нетронутых беспартийных блондинок (N1) плюс количество изнасилованных беспартийных блондинок (N4). Количество партийных, но нетронутых девиц равно количеству нетронутых партийных брюнеток (N3) плюс количество нетронутых партийных блондинок (N2). Количество нетронутых блондинок же равно количеству нетронутых беспартийных блондинок (N1) плюс количество нетронутых партийных блондинок (N2). // очевидно же будет больше, либо равно (в случае, если //. Ясно же, что ни количество нетронутых партийных брюнеток, ни количество изнасилованных беспартийных блондинок не может быть отрицательным! Неравенство Белла доказано.
Теперь представим, что девиц в Петушках не 428, а очень-очень много. Скажем, три миллиарда. И мы их случайным образом поделили на три группы, по миллиарду девиц в каждой, и в каждой группе проводим проверку. Вот только девицы обладают некоторой странностью: из трёх возможных свойств можно проверить только два. Скажем, если содрать с девицы парик, чтобы узнать, блондинка она или нет, а затем проверить наличие партбилета, то уже не остается никакой возможности проверить, изнасилована она или нет. И так далее. Но поскольку группы очень большие и одинаковые, мы можем предположить, что количество блондинок, партийных или изнасилованных во всех группах примерно равно. Тогда в первой группе мы можем посчитать количество беспартийных блондинок, во второй — количество партийных, но нетронутых, а в третьей — количество изнасилованных брюнеток. И с немалой уверенностью можно утверждать, что неравенство Белла для полученных чисел будет соблюдаться.
В квантовой механике же выходит, что количество беспартийных блондинок плюс количество партийных, но нетронутых равно где-то примерно 30% от всех девиц (даже чуть меньше), а количество нетронутых блондинок — где-то 50%. Ну да, 30% конечно же больше либо равно 50%… ЛОЛШТО?! Немая сцена и занавес.
https://lurkmore.wtf/%D0%9A%D0%B2%D0%B0 ... 0%BA%D0%B0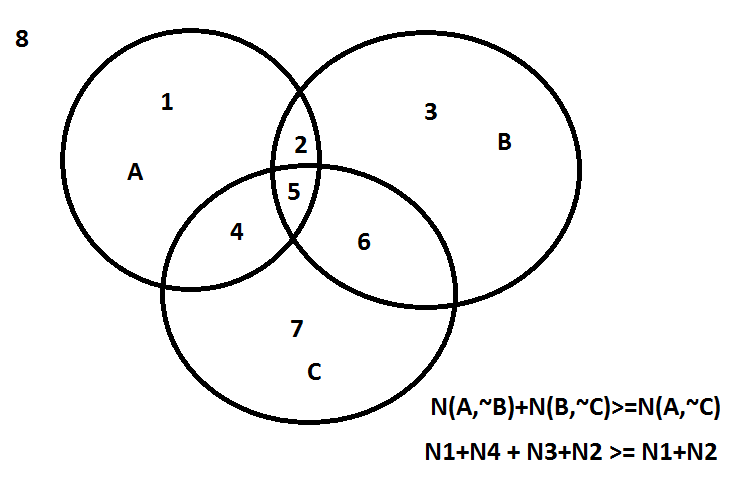
Правильно ли я понял, что на картинке выше с ПГШ A - это блондинки из цитаты, B - соответственно партийные, C - изнасилованные?
Для самых продвинутых ещё вопрос: насколько важно в этой модели учитывать дополнительные измерения из-за того, что квантовая механика имеет дело с комплексными величинами? Извиняюсь если я всё мешаю в кучу, но вот с фотонами я слышал, что поляризация одного фотона формально описывается двумя комплексными числами и поэтому тут надо использовать сферы Блоха:
https://ru.wikipedia.org/wiki/Сфера_Блоха
Если не путаю, неравенства Белла примерно одинаковы для эксперимента с электронами и приборами Штерна-Герлаха и для эксперимента с фотонами и поляризаторами.