А как она с интегралом Курцвейля связана?
А никак. Просто можно смотреть на формулу Ньютона-Лейбница

(где

,
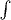
- интеграл Римана) как на частный случай формулы Стокса - можно заменить отрезок на многообразие, а границы отрезка на край, ну и функцию придется менять на дифференциальную форму. А можно на неё же как на частный случай свойства интеграла Курцвейля:

(где

,
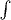
- интеграл Курцвейля) - заменяем интеграл на более общий, и функции можно брать из более широкого класса.
В более общем случае, видимо, явление такое получается.
У нас есть пространства

,

и

,

является подпространством двух других. На

и

есть операторы "интеграл от производной" и "интеграл по границе", причем на

эти операторы соглашаются. Формула Стокса утверждает, что эти операторы совпадают для пространства

, свойства интеграла Курцвейля - что они совпадают для

, формула Ньютона-Лейбница - что они совпадают для

. Какое из утверждений (про

или

) является её обобщением - непонятно.
Возможно, существует какое-то пространство, включающее и

, и

, на которое тоже можно продлить эти два оператора, но я про такое не слышал (что, впрочем, не является особо сильным свидетельством в пользу его отсутствия, я и про интеграл Курцвейля случайно узнал).



