Хочу предложить еще одну табличку Радикалы против Полларда
Хотелось бы на кривой, но лихой козе сначала эту задачу объехать.
Вернусь к классификации

от заданного

, о чем я писал выше. При этом вместо исходного равенства для красоты будем говорить о приближении средним арифметическим, средним геометрическим:

Возьмем произвольное

. Было показано, что

дает приближение для (1) порядка

, при нечетном

, и
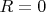
при четном

(его далее рассматривать не будем ввиду тривиальности).
Поскольку для

дает лучшее приближение, то, играясь с четностью

можно получать лучшие приближения для (1) c

при нечетном

и

Рассмотрим примеры. Возьмем к примеру


Наберем разные факторизации:

Ясно, что

- лучшее нижнее приближение.

- ясно, что здесь лучшесть приближения не обязана сработать, поскольку приближаемся с другой стороны

Возьмем оба

четные:

, для них лучшесть приближения обязана сработать.


Таким образом, действительно получаем

оптимально.
Берем другое представление четных:

- опять должно сработать с

.

Какой вывод отсюда следует - это лучшее приближение для

, но это не значит, что это лучшее приближение вообще, поскольку существует

Идем дальше, попробуем минимально ухудшить приближение:

Возьмем все тоже

, тогда имеем:

Здесь без вариантов получаем:

Т.е.

- лучшее приближение в классе

, но оно не лучшее в целом, поскольку для

существует приближение в классе

.
Пробуем далее ухудшать качество:

Поскольку

вынуждено разной четности, а

четное, то ни одна комбинация не обязана сработать.
Все это можно продолжить и далее.



