Диофантово уравнение a^x + b = b^y +a

[AlexanderPlus]

Столкнулся с показательно-диофантовым уравнением

$$a^x + b = b^y + a$$

где $a,b$ - простые числа, $a \ne b$, $x,y$ - целые числа, $x \geqslant 0, y \geqslant 0$

Так как уравнение симметрично относительно замены $a$ на $b$, то для удобства далее принимаю $a > b$

Из очевидного:

1. Пары $\left\lbrace x,y \right\rbrace$:
$\left\lbrace 0, 0 \right\rbrace$ - не является решением, так как дает $b = a$, а по определению $a \ne b$
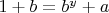
$\left\lbrace x, 0 \right\rbrace$ и $\left\lbrace 0, y \right\rbrace$, где $x > 0, y > 0$ - нет решений, так как дает $a^x + b = 1 + a$ и $1 + b = b^y + a$, а по определению $a > 1, b > 1$
Отсюда $x > 0, y > 0$

2. Элементарное решение $x = 1, y = 1$ для всех $a$ и $b$:

$$a + b = b + a$$

3. Пары $\left\lbrace x,y \right\rbrace$:
$\left\lbrace x, 1 \right\rbrace$ и $\left\lbrace 1, y \right\rbrace$ дает уравнения $a^x + b = b + a$ и $a + b = b^y +a$. После сокращения: $a^x = a$ и $b = b^y$, что дает обратно пару $\left\lbrace 1, 1 \right\rbrace$

4. Остается ситуация $x > 1, y > 1$
Перенесем $a$ и $b$ по разные стороны знака равенства:

$$a^x - a = b^y - b$$

Так как $x > 1, y > 1$, вынесем $a$ и $b$ за скобки

$$a(a^{x-1} - 1) = b(b^{y-1} - 1)$$

Для удобства сделаем замену $u = x-1, v = y-1$
В итоге получается:

$$a(a^u - 1) = b(b^v - 1)$$

где $u > 0, v > 0$

5. Рассмотрим простой случая, когда множители равны попарно:

$$\left\{ \begin{array}{rcl} &a = b^v - 1& \\ &b = a^u - 1& \\ \end{array} \right.$$

так как $a > b$ и $a,b$ - простые числа, то $a$ - нечетное, отсюда $b = a^u - 1$ - четное. То есть $b = 2$
Отсюда $a^u - 1 = 2$ и $a^u = 3$, то есть $a = 3, u = 1$. Подставляя во вторую пару, получаем $v = 2$
В итоге имеем решение оригинального уравнения:

$$3^2 + 2 = 2^3 + 3$$

6. Остается случай, где $k = \gcd(a^u - 1, b^v - 1) > 1$.

$$\left\{ \begin{array}{rcl} &ak = b^v - 1& \\ &bk = a^u - 1& \\ \end{array} \right.$$

Так как $a$ и $b$ - простые числа, то $\gcd(a, b) = 1$, следовательно $(a^u - 1) \mod b = 0$ и $a^u \mod b = 1$. Кроме того $(b^v - 1)$ имеет делитель $(b - 1)$ и по аналогии $a^u \mod (b - 1) = 1$. То есть u делиться на какой-то из делителей $(b - 1)$, а так же на делитель $(b - 2)$
Симметрично для $b^v$.

Вот дальше я застрял. Из общих соображений напрашивается, что больше решений уравнение не имеет, в силу своей симметричности и того факта, что $a \ne b$. Разве что случай с $b = 2$ может подкинуть ещё какой-то сюрприз.
Для конкретных значения $a$ и $b$ отсутсвие решений доказывается просто: из $a^u \mod b = 1$ находим делители u, дальше раскладываем $a^u - 1$ на множители, получаем новый делитель для противоположной части. Повторяем для противоположной части уравнения и так до тех пор пока не придем к противоречию - вот тут описано подробнее.
Для общего же случая, получается, надо или явно придти к противоречию в общем же виде, или же показать что здесь имеет место бесконечный цикл, когда один множитель $x$, порождает новый множитель $y$ и наоборот, и так до бесконечности.

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны небольшие формулы и отдельные обозначения (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[Pphantom]

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (М)»

[Andrey A]

AlexanderPlus в сообщении #1563718 писал(а):

Из общих соображений напрашивается, что больше решений уравнение не имеет...

$13^3+3=3^7+13$

На полное решение тут мало надежды (я бы удивился), но методика поиска решений цепными дробями существует. Хорошо бы понять для начала конечно ли их число.

[AlexanderPlus]

Спасибо

Andrey A в сообщении #1563824 писал(а):

$13^3+3=3^7+13$

Да, получается есть ещё решения. В чем ищете подобные решения?

Andrey A в сообщении #1563824 писал(а):

методика поиска решений цепными дробями существует

Можете подсказать, что почитать на эту тему?

[Andrey A]

Почитать не знаю, это индивидуально. Я читал Хинчина и Гаусса, а лучше самостоятельно поэкспериментировать. Впрочем, была у нас тема Цепные дроби ищу литературу. Ваше уравнение переписываем так: $a^x-b^y=a-b$. Если $\gcd x,y >1$, можем сократить почленно лево и право на $a-b$, и получаем тогда справа единицу, слева — арифметическую сумму нескольких слагаемых. Значит пара $x,y$ взаимно проста. Случаи с малыми числами Вы уже рассмотрели. Для достаточно больших параметров можем нестрого переписать последнее равенство так $a^x \approx b^y$ и, прологарифмировав обе части, так: $x\ln a \approx y\ln b.$ То есть $\log a_b \approx \dfrac{y}{x}.$ Если заранее известно, что для заданной пары $a,b$ решение существует, однозначно находим его разложением $\log a_b$ в цепную дробь (если $x,y$ вз. просты). В моем примере $\dfrac{\ln 13}{\ln 3}=2,2,1,79,...=\dfrac{2}{1},\dfrac{5}{2},\dfrac{7}{3},\dfrac{558}{239},...$ Третья дробь дает решение $13^3-3^7=10=13-3.$ В сущности таким разложением находим "точки сближения" двух степенных рядов. Для Вашего уравнения требуются "сильные" точки сближения, поэтому большой четвертый знак — не случайность. Теоретически решение может быть выражено дробью из пяти знаков, тогда шестой знак должен быть "очень большим". Но крайне маловероятно.
Теперь самое интересное. Если бы уравнение было задано так: $a^x-b^y=\left | a-b \right |$, решений было бы больше (дробь из двух/трех/четырех знаков). Маленькие видны невооруженным глазом: $3^3-5^2=\left | 3-5 \right |;\ 2^7-5^3=\left | 2-5 \right |.$ А так не знаю. Может статься, мой пример уникален ) Конечно ли число решений — вот вопрос.

P.S. Доказать напрямую вз. простоту $x,y$ что-то не удается. Но предположим, существует решение с $\gcd x,y>1.$ Это значит, что в процессе разложения $\log a_b$ получена несократимая дробь $p/q$ такая, что $a-b\ \vdots\ a^q-b^p.$ Для проверки тогда достаточно легкого перебора, поскольку $a^q-b^p<a^{2q}-b^{2p}<a^{3q}-b^{3p}<...$ и т.д. Но на практике такого не встречалось.

[svv]

Перепишем уравнение в виде $n=a^x-a=b^y-b$. Нетривиальное решение означает, что число $n$ представимо в виде $a^x-a$ более чем одним способом.

В OEIS нашлась последовательность:
A057896 — Nonnegative numbers that can be written as m^k-m (with m and k nonnegative) in more than one way.
Список таких чисел, известных на сегодняшний день, невелик:
$0, 6, 30, 210, 240, 2184, 8190, 78120, 24299970$

Зная их, легко найти решения:
$\begin{array}{rcccc}6&=&2^3-2&=&3^2-3\\30&=&2^5-2&=&6^2-6\\210&=&6^3-6&=&15^2-15\\240&=&3^5-3&=&16^2-16\\2184&=&3^7-3&=&13^3-13\\8190&=&2^{13}-2^{\phantom{1}}&=&91^2-91\\78120&=&5^7-5&=&280^2-280\\24299970&=&30^5-30&=&4930^2-4930\end{array}$

Интересны даже краткие комментарии:

Цитата:

The next term, if it exists, is at least 2*10^17.
...
Conjectured to be finite and complete by Bennett (2001).

[Andrey A]

svv в сообщении #1563861 писал(а):

Зная их, легко найти решения:

Интересно. Но для настоящей задачи из этого списка годятся всё те же два примера, ведь $a,b$ у нас простые.
А со степенями $>2$ остается всё тот же единственный. Никто и не говорил что будет легко )

[svv]

Ну, ладно.
Тут ведь как: кто-то был бы рад, если бы ещё нашлись решения. Кто-то, возможно, рад, что они не нашлись. Кто-то будет рад узнать о достигнутых на сегодняшний день результатах. Я же просто привожу информацию.

[Andrey A]

svv
Всё в порядке, все рады. А вот со вз. простотой $x,y$ я, кажется, напутал. В Вашем списке они действительно взаимно просты, но не пойму так ли уж это обязательно (поправил выше).

[AlexanderPlus]

Ух как всё интересно. Спасибо большое всем!

[Andrey A]

Andrey A в сообщении #1563858 писал(а):

... что в процессе разложения $\log a_b$ получена несократимая дробь $p/q$ такая, что $a-b\ \vdots\ a^q-b^p.$

Знаковый пример: $\log {253}_{40}=1,1,1,13116,2,...$ Ограничения на величину знаков либо высоки, либо их вовсе нет. $253-40=213;\ 253^2-40^3=9.$ Если бы еще одно делило другое, можно бы поискать решение с не вз. простыми $x,y$, да и дробь из пяти знаков уже не кажется чем-то невозможным. Проблема полнократных где-то рядом маячит, запахи знакомые )

AlexanderPlus в сообщении #1563979 писал(а):

Ух как всё интересно.

Так дерзайте!