Yadryara, here is a partial worked example run for the 'oul' program in a simple case: ./oul -n 12 3. Specifying "-n" means "no database", so we start with an assumed upper limit of

, and attempt to find

.
We initialise the allocated multiple and outstanding

values:

.
First job is to find fixed primes

, in this case 2 and 3.
Recursion level 0: possible arrangements for powers of 2 over the three elements are precalculated. We initially try the first of those, and set

.
Recursion level 1: possible arrangements for powers of 3 are similarly precalculated. We cannot use any of

in

, so we next try assigning

. But that leaves

, so we check the case

(which fails), and immediately continue to the case

, so we now set

.
Fixed primes are now allocated, so we proceed to the main
recurse().
Recursion level 2: we first decide which

to allocate to, by calling
best_v(). This chooses

, since

is the highest remaining multiple of the highest odd factor dividing
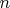
. We now loop over the powers (2, 5, 11) that can satisfy the highest odd factor dividing
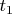
, starting with 2, and then start looping over primes
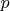
starting with

, the first prime after the fixed primes used above. So we set

and recurse.
Recursion level 3:
best_v() chooses

as the next to allocate to, since

. We now loop over the powers (2, 5) that can satisfy the highest odd factor dividing

, starting with 2, and then start looping over primes
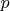
starting with

. We see that

has already been used (and since

, it cannot be used a second time), so advance to

. So we set

and recurse.
Recursion level 4:
best_v() returns nothing, since all

are now powers of 2, so we will call
walk_v() and return.
walk_v() collects the

and

, uses CRT to calculate

, finds

as the least common multiple of the

, calculates

and

.
We have no limit at this point, so we start an infinite loop

such that

. On each iteration of the loop, we first check that

, then

. In this case we get a match with

, yielding

. So we log 870924 as a candidate and return.
Recursion level 3: we now have a limit, so we calculate what the greatest prime we need to check is: in this case that's

. Now we try the next prime

, and call
walk_v() again to find 678324, further reducing our limit
And so we continue until all the recursions complete. By now our best candidate is 1274, and we have checked every factorization that could possibly give a smaller solution, so we declare

.
I hope this makes the approach clear.