наверное все мои проверки были только про 70 делителей
Присмотрелся к 70 делителям.
Для того, чтобы

оказалось равно 4 (больше быть не может), нужно чтобы

и

(обозначения из предыдущего доказательства) вместе входили в цепочку. Удается доказать, что это возможно только при

.
Просмотрел

таких чисел. Результаты неутешительные.
Нашлось 31 значение

c 70-ю делителями. Среди них нет подходящих

. Но, в то же время, есть одно (найденное первым!) значение

, для которого

. (Это

.)
О чем это говорит?
С одной стороны о том, что найти противоречие удастся вряд ли:

, т.е. структура канонического разложения та же, что нужна для 70-и делителей. Только вместо 2-й степени должна быть 6-я (ну или вместо 4-й - 6-я, а вместо 2-й - 4-я).
С другой стороны практически безнадежно искать цепочку длиной 4: шестые степени встречаются гораздо реже квадратов, плюс

и
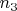
тоже должны иметь по 70 делителей.
В общем, прогноз такой: и не докажем, что не существует, и не найдем.
При этом доказать отсутствие цепочки длиной 4 представляется все же более реальной задачей. Например, среди решений уравнения Пелля, AFAIR, квадраты есть, а 4-х степеней нет. Вдруг тут аналогичная история.