пианист, спасибо за ссылку.
М.В. Федорюк в книге «Метод перевала» писал(а):
3. Интегралы по множествам уровня. Пусть

— вещественнозначная функция и

— множество уровня, заданное уравнением

(

— постоянная),

. Если

непусто и

на

, то это множество является

-мерным

-многообразием в

.
Дифференциальной формой Лере-Гельфанда называется форма

степени

, удовлетворяющая уравнению

Эта форма однозначно определена на

при

, если

на

([26]).
У ТС введены криволинейные координаты

. Допустим, функции преобразования от декартовых координат к криволинейным и обратно гладкие, с ненулевым якобианом. Тогда описанное «разложение типа Лере-Гельфанда» формы объёма

в
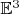
можно записать сразу:


У Федорюка

— не площадь.
Хоть

получена совсем не так, как описано в книге, она удовлетворяет всем условиям.
Проблема в том, что ограничение формы

на

хоть и может играть роль

-формы объёма (т.е. площади) на

, но такая площадь в общем случае не будет согласованной с метрикой
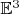
. А, как я понял, автору темы хотелось бы, чтобы тут был именно элемент площади.



