Построение по условию

[pritychka]

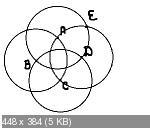
Некоторую точку B плоскости фиксируют как вершину, и из нее радиусом, равным b, описывают дугу окружности. На этой дуге берут две новые точки A и C. Дуга радиуса b, описанная из C, пройдет через B, так как BC=b, согласно только что выполненному построению. Некоторую точку D на этой дуге принимают за новую вершину. Дуга радиуса b, описанная из D, пройдет через C. Чтобы возникающаю в таком построении фигуру сделать замкнутой, новую вершину E нужно взять на этой дуге не произвольно, а так, чтобы она одновременно лежала и на дуге, описанной из точки A радиусом b и проходящей через B; иначе говоря, эта вершина должна определться пересечением двух дуг.

Должно получиться что-то похожее на замкнутую вокруг пентаграммы кривую

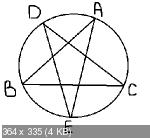
Вот мой "шедевр". Не могу понять, где я нарушил условие

[mihaild]

pritychka в сообщении #1550845 писал(а):

Чтобы возникающаю в таком построении фигуру

Какую фигуру? До того описано только построение 4 точек.

[Emergency]

mihaild в сообщении #1550848 писал(а):

Какую фигуру? До того описано только построение 4 точек.

Ну это же 10-классница писала...

[pritychka]

mihaild в сообщении #1550848 писал(а):

pritychka в сообщении #1550845 писал(а):

Чтобы возникающаю в таком построении фигуру

Какую фигуру? До того описано только построение 4 точек.

Извините, забыл строчку, которая описывает "правильный" результат :
"Таким путем получается пятиугольный дуговой многоугольник ADBEC постоянной ширины."