Меня заинтересовала ниже изложенная тема в математике, и я бы хотел поискать что о ней известно, какие работы по ней велись, но я не знаю как она называется, и какие ключевые слова искать.
У нас есть целое число
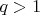
и мы строим

которому относятся все последовательности (

) целых чисел от

до

на позициях от

(любое, и возможно отрицательное) до бесконечности и ноль на позициях меньше

. И число в

можно представить в виде нестандартного

-ичного представления

В отличии от

нули в другой стороне. И добавляем операции

как

(

требуемая операция) когда k стремится к бесконечности.
И добавляем норму для чисел в

, для

у которого
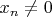
норма будет

, а норма

будет ровна

.



