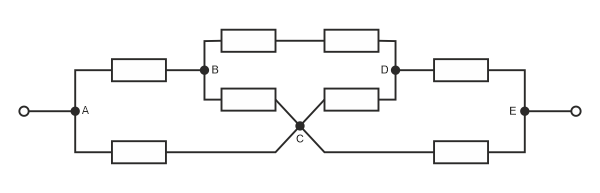
Помогите, пожалуйста, с такой схемой (сопротивления резисторов равны), можно ли её привести (и как это сделать) к виду с очевидной композицией последовательно и параллельно подключенных резисторов?
 Далее оффтоп:
Далее оффтоп:В оригинале задачи более сложная схема, сопротивления всех резисторов одинаковы и равны R, дано напряжение источника U. Требуется найти рассеиваемую мощность.
Получается, сначала нужно найти сопротивление. На картинке кусочек данной в задаче схемы, где у меня не выходит преобразовать её к "стандартному" виду смешанного соединения (с очевидной композицией последовательных и параллельных соединений).
Вот вопрос - это возможно сделать? найти такой эквивалентный вид. Или же нужно как-то по-другому решать?
Предположим, что нет эквивалентной классической схемы, тогда как считать? Я составлял систему по законам Кирхгофа и, в принципе, все нашел. Самое важное из этого имхо - направление движения токов (и вот на картинке в теме - токи на всех участках цепи сонапралены - или слева направо, или наоборот). Но задача школьная, законы Кирхгофа там вроде не формулируются. В оригинале, к примеру, есть вот такой резистор:
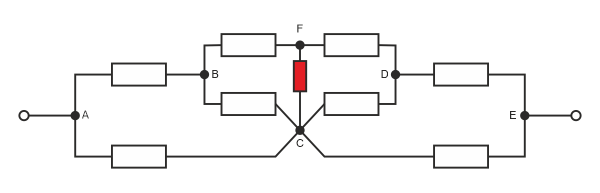
и между узлами F и C напряжение нулевое получается. Я могу объяснить это в терминах потока заряда за единицу времени, рассматривая электричество как воду

Но не соображу как это связать с сопротивлением. Я смотрел несколько учебников с выводом стандартных формул в терминах

, но почти везде авторы "из воздуха" достают постулаты (мол, общее напряжение здесь равно сумме напряжений, а здесь - они равны), что затрудняет понимание того как вывести формулы для сложных цепей.
Простите за большое количество текста, я пытался донести уровень своей некомпетентности в электричестве. Спасибо!



