Точность, абсолютная погрешность и округление

[Pphantom]

misha.physics в сообщении #1534720 писал(а):

Просто интересно, может ли в принципе существовать такой вариант правила округления?

Так не принято делать, но никаких других препятствий нет. Однако без дополнительных пояснений это будет понято неправильно, а смысл всех этих правил в том, чтобы писать поменьше там, где без этого можно обойтись.

[misha.physics]

sergey zhukov,

sergey zhukov в сообщении #1534723 писал(а):

Так вот эта погрешность прибора и превращает результат измерения в случайную величину с распределение Гаусса. Это уже и есть "сложный" случай.

Я просто под погрешностью прибора понимал погрешность, которая написана на самом приборе (или в документах идущих к прибору). И ещё я представлял себе формулу, что абсолютная погрешность равна сумме погрешности прибора и погрешности отсчёта. В свою очередь погрешность отсчёта составляет половину цены деления измерительного прибора.

sergey zhukov в сообщении #1534723 писал(а):

Я записываю $2,72$ с точностью $0,005$.

Хорошо, примем это, тогда как я понимаю можно написать $e=2.72\pm0.005$. И в принципе это логично, потому что при округлении чисел $2.715$, $2.725$ и чисел между ними к сотым мы придём к $2.72$ (если округлим пятерку в разные стороны в первых двух случаях, но это сейчас можно опустить). Но как тогда быть с этим?:

misha.physics в сообщении #1534634 писал(а):

одним из правил округления является то, что количество значащих цифр в результате измерения должно быть таким, чтобы сомнительная цифра имела порядок абсолютной погрешности

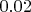
Здесь получается, что если у нас абсолютная погрешность, округлённая к одной значащей цифре имеет, например, порядок сотых ($0.02$ или $0.07$, например), то результат измерения тоже округляется к сотым (например к $42.16$). Или это неправильно? Просто я видел следующий пример. Получили (калькулятор выдал) абсолютною погрешность $\Delta l=3.8485...$. Мы округляем это к одной значащей цифре: $\Delta l=4$. Получили (калькулятор выдал) неокруглённое значение измеряемой величины $l_0=384.8116...$, его мы округляем так, чтобы последняя цифра имела порядок единицы (как абсолютная погрешность), то есть $l_0=385$. И конечный результат записывался как $l=385\pm4$.

[Emergency]

misha.physics в сообщении #1534735 писал(а):

Я просто под погрешностью прибора понимал погрешность, которая написана на самом приборе (или в документах идущих к прибору). И ещё я представлял себе формулу, что абсолютная погрешность равна сумме погрешности прибора и погрешности отсчёта.

Если у прибора есть шкала, то деления в ней наносят так, чтобы половина деления соответствовала паспортной погрешности прибора. Поэтому у приборов высокого класса шкалы длинные, а деления частые. Напротив - у приборов низкого класса шкалы короткие и деления широкие.

[sergey zhukov]

misha.physics
Тут два разных случая. В одном из них - округление точного числа $e$, в котором нет никаких сомнительных чисел ни в каком знаке после запятой. В другом случае - округление результата измерения, для которого существует неопределенность, вероятность и "сомнительные" разряды. Очевидно, что точность округления до половины младшего разряда - это предельно высокая точность записи числа вообще. Она достижима только для округления совершенно точных чисел, а результат измерения не является совершенно точным. Соответственно, его запись с погрешностью должна отражать этот факт, а не выглядеть, как округление совершенно точного числа.

[misha.physics]

Emergency в сообщении #1534746 писал(а):

Если у прибора есть шкала, то деления в ней наносят так, чтобы половина деления соответствовала паспортной погрешности прибора. Поэтому у приборов высокого класса шкалы длинные, а деления частые. Напротив - у приборов низкого класса шкалы короткие и деления широкие.

Если я правильно понял, имелось ввиду, что погрешность округления (половина деления) равна погрешности прибора (паспортной погрешности). Просто опять же видел решение задачи, где брался медицинский термометр, на нём было написано $0.1^\circ C$ и это было взято за погрешность прибора, цена деления прибора тоже была равна $0.1^\circ C$, поэтому за погрешность округления было взято половину: $0.05^\circ C$. И абсолютная погрешность получилась равной сумме этих погрешностей, то есть $0.15^\circ C$.

sergey zhukov, спасибо. Хорошо, то есть можно сказать, что когда мы говорим, что точность табличного значения какой-то величины равна половине единицы младшего разряда, то можно считать, что эту величину сначала как-то измерили с большей точностью (с большим количеством цифр), а потом для таблицы просто округлили к меньшему количеству значащих цифр. То есть здесь есть лишь погрешность округления. А когда мы сами измеряем какую-то величину, то могут быть другие погрешности, поэтому погрешность больше. И это всё вместе с тем, что могут существовать разные варианты правила округления. Хорошо, в принципе стало понятнее.

[Emergency]

misha.physics в сообщении #1534819 писал(а):

Если я правильно понял, имелось ввиду, что погрешность округления (половина деления) равна погрешности прибора (паспортной погрешности).

Погрешность округления бывает в расчетах, а не в считывании шкал.
Медицина - это не то на что стоит ориентироваться в измерениях, и вряд ли вы сможете опубликовать научную статью про тепловые эффекты реакций, указав в качестве измерительного прибора медицинский термометр. Но есть вы пользуетесь поверенными измерительными приборами высокого класса с зеркальной шкалой, то смело можете указывать показания с точность до половины деления (не округляя). То есть, если цена деления миллиамперметра составляет 1 мА, то измеренное значение 34,5 мА будет правильным, а 34,2 - неправильным.

[misha.physics]

Спасибо.

[misha.physics]

Я ещё придумал пример.
Пусть мы получили результат измерения $l_0=1374,27\ \text{м}$ и абсолютную погрешность $\Delta l=8,34\ \text{м}$ (случайной погрешности нет). Округляем погрешность к одной значащей цифре: $\Delta l=8\ \text{м}$ и округляем результат измерения к младшему разряду абсолютной погрешности: $l_0=1374\ \text{м}$. Тогда $l=(1374\pm8)\ \text{м}$. Пусть мы хотим привести этот результат в таблице, но без указания абсолютной погрешности. Получается, что если мы примем соглашение, что погрешность результатов, приведённых в таблице равна половине единицы разряда сомнительной цифры (последней цифры) или даже единице разряда сомнительной цифры, то мы не можем указать наш результат в таблице ни как $1,374\cdot10^3\ \text{м}$, ни даже как $1,37\cdot10^3\ \text{м}$. Тогда что делать, округлить "ещё сильнее" и писать в таблице $1,4\cdot10^3\ \text{м}$ или придумывать другое соглашение "считывания" погрешности из данных, приведённых в таблице?

[Pphantom]

misha.physics в сообщении #1535396 писал(а):

Получается, что если мы примем соглашение, что погрешность результатов, приведённых в таблице равна половине единицы разряда сомнительной цифры (последней цифры) или даже единице разряда сомнительной цифры, то мы не можем указать наш результат в таблице ни как $1,374\cdot10^3\ \text{м}$, ни даже как $1,37\cdot10^3\ \text{м}$.

Почему? Для правильной порядковой оценки погрешности вполне сойдет второй вариант.

[misha.physics]

Pphantom в сообщении #1535398 писал(а):

Почему? Для правильной порядковой оценки погрешности вполне сойдет второй вариант.

Я рассуждаю так, если мы напишем в таблице $1,37\cdot10^3\ \text{м}$ и договоримся, что погрешностью будет даже единица разряда сомнительной цифры, то есть погрешностью будет $10\ \text{м}$, то получится, что истинное значение величины $l$ находится в отрезке $[1,36\cdot10^3\ \text{м};1,38\cdot10^3\ \text{м}]$. А если мы вспомним, что раньше у нас было:

misha.physics в сообщении #1535396 писал(а):

Тогда $l=(1374\pm8)\ \text{м}$.

то, например, значение $(1374+8)\ \text{м}=1382\ \text{м}$ не принадлежит отрезку $[1,36\cdot10^3\ \text{м};1,38\cdot10^3\ \text{м}]$.

[Pphantom]

misha.physics, я же уже писал: это порядковая оценка. Если для вас важна (действительно важна) разница между погрешностью 8 м и 10 м, то такие методы попросту не годятся, надо честно указывать погрешность (причем, возможно, несимметричную, и с явным указанием метода ее оценки).

[misha.physics]

Pphantom, спасибо, хорошо, мне правда непросто привыкнуть к этому.

[sergey zhukov]

misha.physics
У нас задано число, распределенное на отрезке шириной $16$ метров. А в десятичной системе оборванное число распределено на отрезке, равном одному младшему разряду, т.е. на отрезке либо $10$, либо $100$ метров (ближайшие подходящие варианты). Если мы хотим, чтобы первый диапазон непременно уложился во второй, то придется брать $100$ метров, т.е. писать $1,4\times 10^3$ метров.

Но это просто какая-то неправильная таблица получится. В ней величина погрешности измерения чрезмерно огрубляется до степени 10. А как же все остальные промежуточные варианты величины погрешности? В хорошей таблице так грубо не станут писать.

[sergey zhukov]

wrest в сообщении #1534646 писал(а):

Но так и не понял как можно намерить диаметр десять штангенциркулем, у прутка диаметром пять...

Я думаю, гауссиана - это асимптотическое приближение для суммы конечного числа случайных величин, каждая из которых имеет конечное распределение (например, равномерное), где число этих величин стремится к бесконечности. Например, гауссиана отлично приближает биномиальное распределение (распределение суммы случайных величин, каждая из которых имеет конечное распределение вида 1 - 0.5, 0 - 0.5).
Если взять $N$ случайных величин, каждая из которых имеет равномерное распределение на интервале -1...1 и найти распределение их суммы, то с одной стороны, вероятность отклонения этой суммы от нуля на величину более $N$ в точности нулевая, а с другой - гауссиана описывает это распределение все точнее и точнее с ростом $N$. Так что в реальности, я думаю, мы имеем дело все же с конечными $N$ и ограниченными распределениями, а гауссиана - это идеализация, асимптота для бесконечности.

[Александрович]

sergey zhukov в сообщении #1535416 писал(а):

Так что в реальности, я думаю, мы имеем дело все же с конечными и ограниченными распределениями, а гауссиана - это идеализация

Любое аналитически заданное распределение - идеализация.