Допустим, что два заряда электрического диполя размещены не на оси

, а на оси

. Введем сферическую систему координат такую, что координаты декартовы будут равны:
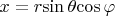
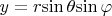
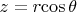
Пусть заряды располагаются на некотором расстоянии друг от друга

, на оси

с одинаковыми расстояниями от начала координат, положительный слева, отрицательный справа

, тогда координаты зарядов будут равны:
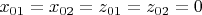
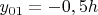
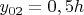
, откуда можно вычислить сферические координаты зарядов:
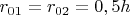
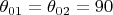
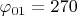
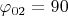
Задача заключается в вычислении потенциала электрического поля, для чего можно использовать принцип суперпозиции:
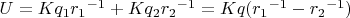
, где
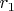
и
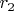
- расстояния от точки, в которой наблюдается поле, до первого и второго зарядов соответственно. Таким образом, задача нахождения потенциала заключается в выражении расстояний от точки наблюдения до зарядов через расстояние до начала координат

, широту
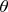
и долготу
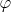
. Используем формулу расстояния
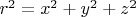
и формулы переноса начала координат в точку первого и в точку второго заряда
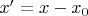
,
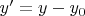
и
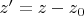
, выражения декартовых координат через сферические и вычисленные сферические координаты обеих зарядов, тогда обратное расстояние от первого до заряда точки, в которой наблюдается поле, равно
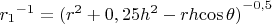
, а от второго
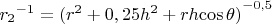
.
Чтобы вычислить компоненты электрического поля, используем формулы градиента в сферических координатах:
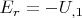
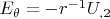
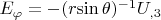
, откуда компоненты такого поля будут равны
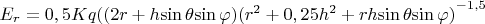
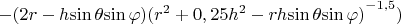
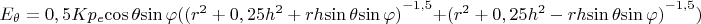
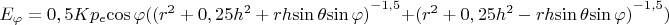
Предположим, как и при обычном вычислении диполя, что расстояние до точки наблюдения поля

намного больше расстояния между зарядами

, и тогда эти выражения упрощаются:
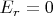
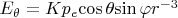
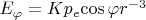
Что дает (по формуле ротора в сферических координатах) ненулевой ротор такого поля
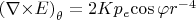
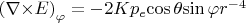
, однако при вычислении от точной формулы он нулевой, как и должно быть для потенциального поля.
Если же разместить заряды и считать поле как обычно, то ротор будет нулевым и для точного, и для приближенного случая. Почему же здесь получается иначе?