соответственно они получены через множество опытов по их измерению
над подготовленном ансамбле систем, находящихся в определенном (изучаемом) состоянии. Да.
Соответственно, померяю координату, найду стандартное отклонение, по идее ипульс надо попробовать одновременно, но как точно не могу сейчас сказать(и не уверен, что возможно прямо одновременно).
нет, нет. У вас есть ансамбль систем, находящихся в определенном квантовом состоянии. Над каждой системой вы можете произвести отдельно измерение либо координаты, либо импульса, но не одновременно обеих наблюдаемых. Дальше вы набираете статистику и строите гистограммы для координаты и для импульса. У каждого столбика на, скажем, координатной гистограмме будет своя ширина, назовем ее
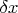
(соответственно

для столбиков импульсной гистограммы). Она соответствует погрешности прибора (на самом деле лучше ее связать с resolution of measurement). Так вот, когда вы собрали статистику и построили две гистограммы, по ним вы уже можете линейкой определить

и

и увидите, что соотношение неопределенностей выполнено (для некоторых специальных квантовых состояний оно будет выполнено как равенство, т.е. есть состояния которые
минимизируют это соотношение). Одной из распространенных ошибок является отождествление

и
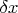
, когда считают, что посчитать

'ы и проверить соотношение неопределенностей можно чуть ли не одним измерением. Кроме того, есть распространенное заблуждение о том, что нижняя граница налагаемая соотношением неопределенности на

и

недостижима для измерительных приборов, что тоже не соответствует действительности. Конечно, для того, чтобы экспериментально проверить соотношение неопределенностей, необходимо чтобы
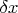
и

были меньше чем соответствующие

и

.
Ага, из-за физических ограничений как я понимаю? Имеет ли это смысл делать математически?
ну мы же с вами физику обсуждаем. Еще раз повторюсь, физически не имеет смысла говорить о

порядка и меньше, чем комптоновская длина волны. А если

теряет смысл для конкретной квантовой системы на каких-то масштабах, то и любое математическое соотношение, в которое оно входит, теряет свой смысл. Конечно, в просторечии всегда можно сказать "когда

стремится к нулю,

стремится к бесконечности, и наоборот", но всегда нужно понимать границы применимости таких выражений и что их не нужно понимать буквально.