Если мы теперь выберем

произвольно (независимо от

), то может случиться так, что на одной части пути

тело будет двигаться со скоростью

, а на другой

со скоростью

и тогда

не сможет равняться

.
А никто и не обещал, что до точки

тело будет двигаться со скоростью

.
Возможно два варианта.
Либо

, тогда тело движется со скоростью

до точки

, и дальше с этой скоростью,
а после точки

, со скоростью

.
Тогда мы выпиливаем участок пути до

, отсчитав ее от точки старта,
и переходим к более простой задаче нахождения средней скорости, считая что тело начало двигаться
из точки

.
Либо

, и тогда мы можем отпилить участок пути

, отсчитав его от точки финиша назад.
И снова возвращаемся к более простой задаче, где со старта тело движется до точки

со скоростью

,
и от

до точки

со скоростью

.
Оба этих варианта, таким образом, сводятся к задаче, в которой

,
то-есть когда тело движется до точки

, со скоростью

, и от этой точки со скоростью

.
И нам нужно пересчитать условия задачи к этому случаю, потому что при удалении ненужной нам части пути изменятся

, и

, а также

, и

, и

.
И эта

, часть всего пути, которую тело пройдет со скоростью

, - самая важная величина для решения этой задачи.
Если у меня получится вставить картинку, там будет более понятно всё.
-- Пт июн 04, 2021 20:42:01 --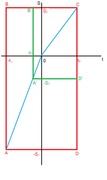
Ну, вроде как, получилось вставить картинку.
Вот Вам "дорожная карта" для решения этой задачи в общем виде.
Для простоты и удобства я сразу перенес начало координат в точку, где изменяется скорость движущегося тела.
Для начала решения, умело пользуясь альфой, мы строим красный прямоугольник, отложив соответствующие

, и

, влево и вправо от нуля по оси абсцисс.
Это будет ширина красного прямоугольника.
Вычислив по альфе - гамму, соответственно по оси ординат откладываем:
вниз

, вверх -

,
это будет высота красного прямоугольника.
Диагональ красного прямоугольника

, покажет нам среднюю скорость на пути

за время

.
(Диагональ я нарисовать забыл, но тангенс угла ее наклона к оси абсцисс
есть средняя скорость на пути

за время

).
Теперь расчехляем бету, и находим

, а по известным

и

вычисляем

.
Наносим на карту красно - зеленый прямоугольник

.
Его диагональ

(забыл нарисовать!

) даст искомую среднюю скорость
на участке

.

.
Как-то так...



