Здравствуйте. Читаю сейчас "Введение в алгебру" Кострикина. Наткнулся на следующее упражнение:
Пусть
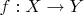
- отображение и

для некоторого

.
Прообраз

иногда называют ещё слоем над элементом

. Показать, что всё множествоX является объединением непересекающихся слоев.
Предупреждение. Обозначение

не следует ассоциировать с обратным отображением, которого может и не быть.
Т.к. не было указано какое именно отображение рассматривается в задаче я начал перебирать все типы. Начал с инъективных:
1.) Пусть
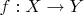
- инъективно, но не сюръективно. Возьмём

.В силу инъективности слои будут состоять из одного элемента и неравенство

можно понимать как

. По определению инъективности при

. Тогда можно сказать что

(подразумевая здесь и далее, что это дизъюнктное объединение)
2.) Для биекции из рассуждений выше очевидно

Если же отображение неинъективное, то начинаются проблемы. Можно, конечно, взять отображение

, которое ставит

в соответствие

и доказать для него, но если взять отображение

, где

, то не о каком дизъюнктом объединение слоёв не идёт и речи.
Это неточность в задаче или я чего-то не понимаю?