Вот такой вопрос возник при решении задачи для 7 класса.
Условие: В исходном состоянии система закрепленных труб с площадью сечения

и

, а также вставленных в них поршней и пружин, которые прикреплены к поршням, находится в покое. Между поршнями находится невесомая жидкость. Левый конец пружины жесткостью

и правый конец пружины жесткостью

закреплены. Пружина жесткостью

сжата на 5 см. На сколько сантиметров сжата пружина жесткостью

? Атмосферное давление

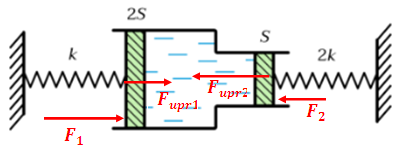
Если решать через равновесие давлений, то в результате сокращаются

и получается числовое решение:


Если решать через равновесие сил, то ничего не сокращается.



В связи с этим вопрос. А можно ли так решать, то есть рассматривать равновесие давлений?
В гугле (буквально) по словосочетанию "равновесие сил" находится 94 тыс. ссылок, а по "равновесие давлений" всего 1.3 тыс.
Или в решении через равновесие сил есть какая-то ошибка?
-- 14.04.2021, 17:46 --Если жидкость невесомая, то давление жидкости в любой точке одно и то же?



