Максимальная возможная разность между вычетами ПСВ(p\#)

[vicvolf]

Dmitriy40
Значит математическая модель образования функции расстояния для всего ПСВ отличается от образования расстояния на интервале $(1,p^2_{r+1})$.

Дело в том, что на интервале $[p^2_r,p^2_{r+1})$ на $r$ -ом шаге решета Эратосфена могут удаляться только вычеты $p^2_r$ и $p_r \cdot p_{r+1}$, которые точно меньше $p^2_{r+1}$, а уже вычет $p_r \cdot p_{r+2}$ входит в этот интервал только в одном случае, когда $p_r=3$, а при больших $p_r$ уже не входит.

Другое дело в полном ПСВ$p_r\#$. Туда входит и $p_r \cdot p_{r+2}$ и многие другие, поэтому вероятность события - попасть на интервал $2p_r$ в ПСВ$p_{r-1}\#$ значительно больше. И за счет присоединения достаточно больших интервалов слева и справа получается большой скачок в максимальном расстоянии на следующем шаге решета вплоть до $3p_r$. Затем полученное расстояние с большой вероятностью будет объединяться с другими большими расстояниями слева и справа и мы получим расстояние $4p_r$ и больше. Процесс увеличения расстояния зависит только от шага решета и не ограничен.

Dmitriy40 в сообщении #1513870 писал(а):

А на $(1;p_{r+1}^2)$ всё проще и малоинтересно.

Не согласен с Вами. Там находятся только простые числа, а в отношении их существует куча гипотез о максимальном расстоянии между соседними и среди них открытая проблема Лежандра. Существует оценки максимального расстояния между соседними простыми числами, но они не дают решение проблемы Лежандра. Естественно стремление улучшить эти оценки.

Впрочем, если Вы считаете, что там все просто, то какие у Вас мысли по оценке максимального расстояния между соседними простыми числами для данного интервала?

[Dmitriy40]

Вот такие мысли:

Dmitriy40 в сообщении #1510341 писал(а):

Вот начало таблицы для интервала от следующего простого до его же квадрата, показываю только моменты смены любого из двух чисел:

Используется синтаксис Text

5#:     6       23
7#:     8       89
11#:    14      113
23#:    18      523
29#:    20      887
31#:    34      1327
97#:    36      9551
113#:   44      15683
139#:   52      19609
173#:   72      31397
389#:   86      155921
599#:   96      360653
607#:   112     370261
701#:   114     492113
1153#:  118     1349533
1163#:  132     1357201
1409#:  148     2010733
2153#:  154     4652353
4129#:  180     17051707
4561#:  210     20831323

Судя по почти полному совпадению с A002386 смена происходит на каких-то простых. По формулам из неё и по ссылкам на подобные можно узнать много интересного ... Типа что оно равно разности между простыми ...

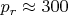Видно что нетрудно посчитать даже для десятитысячных праймориалов, хотя функция Якобсталя посчитана лишь до $p_r\approx300$. Это и есть легко в моём понимании. А что просто — так ведь там легко прямо проверить как будут интервалы формироваться, не так уж их там много, это не весь $p_r\#$.

-- 11.04.2021, 18:17 --

Для некоторых интервалов у меня выше была неправильно указана левая граница, при этом списки остатков правильные, ошибка вкралась лишь при отображении величины границы. Везде где нашёл поправил.

[Dmitriy40]

Варьируя подстроечные параметры алгоритма увеличил интервал для $p_r=9241$ с
$p_r=9241, d=47118$, $4p_{r+1}=37028, d/p_{r+1}=5.089986$, $4p_{r-2}-2=36906, d/(4p_{r-2}-2)=1.276703$, $936124347317291..231791820819473+47118$
до
$p_r=9241, d=48516$, $4p_{r+1}=37028, d/p_{r+1}=5.241007$, $4p_{r-2}-2=36906, d/(4p_{r-2}-2)=1.314583$, $666314641521243..278710494051341+48516$

[vicvolf]

Dmitriy40 в сообщении #1513925 писал(а):

Варьируя подстроечные параметры алгоритма увеличил интервал для $p_r=9241$ с
$p_r=9241, d=47118$, $4p_{r+1}=37028, d/p_{r+1}=5.089986$, $4p_{r-2}-2=36906, d/(4p_{r-2}-2)=1.276703$, $936124347317291..231791820819473+47118$
до
$p_r=9241, d=48516$, $4p_{r+1}=37028, d/p_{r+1}=5.241007$, $4p_{r-2}-2=36906, d/(4p_{r-2}-2)=1.314583$, $666314641521243..278710494051341+48516$

Чем больше $p_r$, тем больше проявляется нелинейность функции Якобсталя.

[vorvalm]

Dmitriy40 в сообщении #1513925 писал(а):

Варьируя подстроечные параметры алгоритма увеличил интервал для $p_r=9241$ с
$p_r=9241, d=47118$, $4p_{r+1}=37028, d/p_{r+1}=5.089986$, $4p_{r-2}-2=36906, d/(4p_{r-2}-2)=1.276703$, $936124347317291..231791820819473+47118$
до
$p_r=9241, d=48516$, $4p_{r+1}=37028, d/p_{r+1}=5.241007$, $4p_{r-2}-2=36906, d/(4p_{r-2}-2)=1.314583$, $666314641521243..278710494051341+48516$

А я думаю, что $d/p_{r+1} \rightarrow 6.$

[Dmitriy40]

vorvalm
Есть ограничение снизу и оно растёт с ростом $r$. А значит когда-то превысит и $6$, и $666$ и $666^{666}$ и вообще любую конечную цифру. Что сложного в понимании этого? Ах ну да, вы же не верите в чужие выкладки, а почитать пару страниц pdf источника и перепроверить самому вывод формулы религия не позволяет ...
Или Вы так и будете каждый раз увеличивать на единицу каждый новый найденный мною порог? Я ведь и $>6$ могу найти, только это долго и мне лень. Вы же и в $>4$ не верили.
Ну и вдогонку, "я думаю" не является ни доказательством, ни даже обоснованием. Я вот думаю оно точно превысит $6$. И что? Я то своё утверждение могу доказать (хотя бы конкретным примером), а Вы своё?

[vorvalm]

Я исходил из того, что расстояния между вычетами в цепочке простых чисел
может быть $2p $ или $4p$. ($2p$ я сразу исключил).
При разности между вычетами ПСВ($p_r\#$) равной $4p_{r+1}$, цепочка чисел кратных $p_{r+1}$ может занимать два положения.
1. Вычеты ПСВ , образующие разность $4p_{r+1}$ кратны $p_{r+1}$ то
сама разность свободна от вычетов кратных $p_{r+1}$
2. Во всех других случаях в разности будут 1 или 2 вычета, кратных $p_{r+1}$
То, что один вычет цепочки кратных $p_{r+1}$ может быть кратным числам модуля
доказана практикой Dmitriy40.
А вот может ли быть таким же кратным второй вычет цепочки, если он есть в разности ?
Мне кажется, что практически это выяснить очень сложно, но есть вариант, который
может решить эту проблему.
Для этого надо рассмотреть разность $6p_{r+1}.$ В этой разности всегда есть 2 вычета кратных $p_{r+1}$.
И если $d/p_{r+1} > 6,$ то это значит, что оба вычета кратны числам модуля

[Dmitriy40]

Почему исключили $2p$ если как показывает опыт они есть?
В остальном ощущение что всё ваше утверждение сводится примерно к "если a=b, то a=b", т.е. тавтологии. Где обоснование что другого (больше) быть не может?
Ну и ваше предположение противоречит результату Pintz (а на самом деле кажется даже не его, формула следует из совсем другой теоремы о простых числах), а значит скорее всего неверно. Да, он(а) тоже мог(ла) ошибиться, но вероятность этого на порядки ниже ошибки у вас.

[vorvalm]

Dmitriy40 в сообщении #1514003 писал(а):

Почему исключили $2p$ если как показывает опыт они есть?

Да, есть конечно. Например в AO48670 (d=106, d=118), но это никому неинтересно.
А в остальном ощущения иногда посещают и меня.

[vicvolf]

Dmitriy40 в сообщении #1514003 писал(а):

Почему исключили $2p$ если как показывает опыт они есть?

А есть ли они на интервале $(1,p^2_{r+1})$?

[vorvalm]

vicvolf
Разговор шел о разностях на интервале $p_r\#$

[Dmitriy40]

vorvalm
Ну что, вот вам и больше шести:
$p_r=39541, p_{r+1}=39551$, $d=240024, d/p_{r+1}=6.068721$, $817189669286826..238121788666729+240024$
$p_r=48121, p_{r+1}=48131$, $d=300330, d/p_{r+1}=6.239845$, $906509255381272..808444150515369+300330$
Сколько теперь будете "думать", семь или сразу восемь, а? Скорее всего я и их найду за разумное время ...

[vorvalm]

Dmitriy40
Моему восхищению нет предела. Это что-то космическое.
Вопросов по этой теме у меня больше нет. Можно закрывать.

[vicvolf]

vorvalm в сообщении #1514025 писал(а):

vicvolf
Разговор шел о разностях на интервале $p_r\#$

Я понимаю, но меня интересует этот кусок ПСВ. Уточню вопрос - есть ли расстояния равные $2p_r$ в ПСВ$p_r\#$ на интервале $(p^2_r,p^2_{r+1})$? По-моему нет.

[vorvalm]

vicvolf
Этот "кусок ПСВ" интересует не только вас. Это же простые числа, но являются вычетами ПСВ.
Без знания общих закономерностей распределения вычетов ПСВ невозможно найти эти закономерности
на отдельных участках ПСВ И чем меньше участок, тем сложнее.