Мы с ув.
Someone обсуждали в личном чате варианты подсчета общего кол-ва позиций в игре, как всех, так и по правилам. Выношу на общее обсуждение.
Пусть оценка
всех возможных позиций сверху будет X. Посчитать ее несложно. Пусть корабли выходят за пределы поля, пересекаются, касаются и пр. Главное, чтобы начальная координата принадлежала полю

Тогда X, число всех возможных размещений 10 кораблей можно посчитать как:

Только меня

смущает. Хотя не надо забывать, что корабль может иметь 4 ориентации, если ориентироваться на одну координату при его создании.
Оценку снизу комбинаторикой найти крайне сложно, если вообще возможно. Поэтому прибегаем к методу Монте-Карло: генерим позиции, легко вычисляемые теорией, а затем компьютером ищем среди них легальные. Доля "легальных позиций" деленная на "все позиции", вычисленное программой, пусть будет К.

и будет искомой величиной "всех легальных позиций в игре". И чем точнее наш коэффициент К (и если он сходится и распределение нормальное), тем точнее будет оценка.
Я написал программу, которая генерирует начальные позиции кораблей, а потом вычисляет легальные, т.е. размещенные по правилам. На

позиций (сейчас запустил на

) выходит только

разрешенных.
То есть генерация самая простая, как только возможно: в любое место, даже не проверяется, попала ли генерированная координата в место, занятое другим кораблем (это проверяется потом). Зато и вычисление в теории всех позиция упрощается, потому что не нужно учитывать клетки, занятые уже и соприкосновения. Ваш алгоритм интересен, но сложен, поэтому возможна ошибка при реализации.
Самое важно, я понял, что нет необходимости генерировать все поле. Какая разница, одна ошибка будет на нем или много? Все равно брак. Достаточно поле генерировать до ПЕРВОЙ ошибки. Это сильно (на пару порядков) увеличило скорость генерации.
1. Генерируем случайную координату. Координаты сначала по вертикали сверху вниз от 0 до 9, потом по горизонтали слева направо от 0 до 9. Сначала "y" в промежутке [0,9], затем "x" [0,9].
2. Генерируем случайно направление корабля [1,4] - вверх, вниз, влево, вправо.
3. Пробуем "вписать" корабль в поле. Если получается (не выходит за пределы), далее. Иначе тут же прерываемся.
4. Если корабль вписался, проверяем его на контакт с уже созданными кораблями. Если не получается, прерываемся. Иначе повторяем (1) до создания полного флота.
5. Когда генерация заканчивается, определяем долю "легальных" позиций, сгенерированных по правилам, как "число позиций по правилам" деленное на "число всех позиций".
Таким образом, при генерации корабли размещаются случайно и независимо. Могут не просто касаться друг друга, а создаваться по тем же координатам, что и уже существующие.
Теперь что получается.
Всего сгенерировано:

правильных:776 доля:0.00000776
Всего сгенерировано:

правильных:7540 доля:0,00000754
Всего сгенерировано:

правильных:76139 доля:0.0000076139
Сейчас генерю

позиций, это на сутки. Думаю, выборка немалая, если считать, что всего позиций ~

, а легальных ~

ГПСЧ - "вихрь Мерсенна", у него безумный период и доказанная равномерность распределения. Начальная затравка - число миллисекунд с 1970 года плюс некоторый случайный "разогрев".
Мне важно понять, сколько легальных позиций в игре, чтобы оценить, насколько мои типичные выборки (

) представительны.
Цитата:
Ничего сказать не могу по этому поводу, кроме того, что доля "отходов" существенно зависит от способа генерации. Более того, оценку сверху можно уменьшить ещё почти в

раз, если учесть, что левая верхняя клетка, скажем, двухпалубного корабля может занимать только одну из

позиций, трёхпалубного — одну из

, четырёхпалубного — одну из

(и каждый из этих

кораблей имеет

ориентации): число возможных расстановок заведомо не превосходит

Это число можно ещё уменьшить, но рассуждения становятся громоздкими, а результат вряд ли будет впечатляющим.
Приведённой здесь формуле соответствовал бы такой алгоритм генерации.
1) Выбираем

попарно различные клетки из полного квадрата

для однопалубных кораблей.
2) Выбираем

попарно различные клетки из левого верхнего квадрата

для левых верхних клеток двухпалубных кораблей, не обращая внимания на

ранее выбранные клетки. Проверяем совпадения клеток (

пар). Если они есть, засчитываем попытку как неудачную и переходим к следующей попытке (к пункту 1).
3) Выбираем

различные клетки из левого верхнего квадрата

для трёхпалубных кораблей, не обращая внимания на

ранее выбранных клеток. Проверяем совпадения клеток (

пар). Если они есть, засчитываем попытку как неудачную и переходим к следующей попытке (к пункту 1).
4) Выбираем

клетку из квадрата
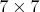
, не обращая внимания на

ранее выбранных клеток. Проверяем совпадения клеток (

пар). Если они есть, засчитываем попытку как неудачную и переходим к следующей попытке (к пункту 1).
5) Выбираем ориентации для

последних кораблей (возможны

ориентации каждого корабля: направо или вниз от выбранной клетки).
6) Проверяем построенную расстановку на соответствие правилам. Если какие-нибудь корабли пересекаются или соприкасаются, засчитываем попытку как неудачную и переходим к следующей попытке (к пункту 1). Вылезть за границу поля при таком способе расстановок корабли не могут.
7) Засчитываем попытку как удачную, прибавив

к соответствующему счётчику, определяем общее число попыток и решаем вопрос о продолжении или окончании расчётов.
Проверять полученные расстановки на совпадения можно, но если Вас интересует доля удачных попыток среди всех попыток, то отбрасывание совпадений должно происходить после прибавления

в пункте 7), а для числа сгенерированных различных позиций нужно завести отдельный счётчик. Это, кстати, позволит оценить и вероятность совпадений. И, конечно, чтобы оценка числа возможных позиций была достаточно надёжной, число сгенерированных различных позиций должно быть достаточно большим.
P.S. Кстати, при использовании всяких генераторов псевдослучайных чисел категорически рекомендуется использовать только малую часть периода генератора.