Взгляните на изображение:
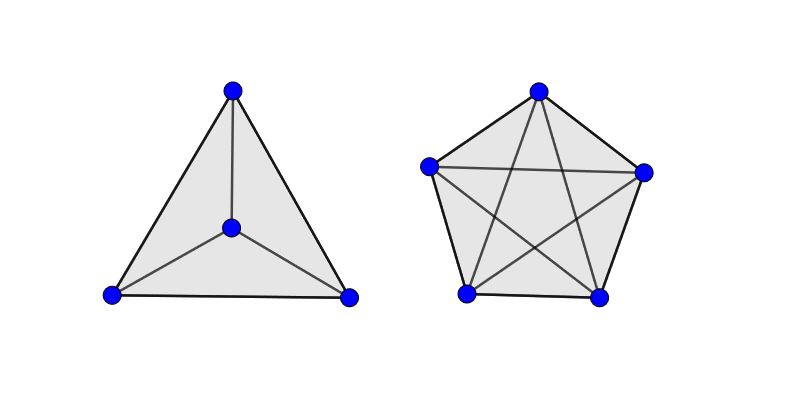
С геометрической точки зрения это ортогональные проекции правильного пятиячейника на плоскости Коксетера

и

соответственно, а с точки зрения теории графов это диаграммы полных графов

и

, то есть задача нахождения числа Рамсея

эквивалентна параметризации произвольного пятиячейника. И в геометрии она уже давно решена. В
этой публикации доказано, что существует ровно

арифметических групп треугольников общего вида и

арифметические группы паракомпактных прямоугольных треугольников, что в сумме даёт искомое

— произвольный пятиячейник не может быть однозначно определён на плоскости меньшим количеством групп, а необходимости в уточнении паракомпактных групп прямоугольных треугольников их компактными группами нет.
Можно доказать и через графы, основные моменты:
1.

это

с добавлением одной вершины и четырёх ребёр.
2.

имеет

вершины и

рёбер - полный набор двухбуквенных слов над четырёхбуквенным алфавитом. На основе множества ребёр

строим

c

рёбрами - делаем их вершинами графа в котором будем искать монохромную клику.
3. Объединяем две копии

в

, у которого

рёбер - добавляем их к

вершинам из предыдущего пункта, получаем граф имеющий

вершины.
4.

имеет

независимых набора рёбер.
5.

, то есть существует ровно

различных функции от набора из четырех элементов до надлежащего подмножества того же набора.
...
Profit!
Хочу также публично обратиться к модераторам: прошу вернуть из Пургатория(М) темы
https://dxdy.ru/topic144557.html и
https://dxdy.ru/topic144583.html. Идея оптимизирующей рекурсии верна, моя ошибка заключалась в том, что для

число оптимизирующей рекурсии

, а не

- следовательно, оптимизирующая рекурсия должна уменьшать интервалы оценок только с их верхних границ; я хотел бы развивать эту идею дальше и иметь возможность для дискуссии. Доказательство гипотезы Коллатца в соответствующей теме верно безусловно, но требует разъяснений; я хотел бы получить возможность эти разъяснения дать.