Задачи из линейной алгебры

[tdk]

Здравствуйте!
Помогите, пожалуйста, решить следующие задания:
1) Найти размерности и базисы суммы и пересечения подпространств
$L_1 = < a_1, a_2, a_3 > $ и $L_2 = < b_1, b_2, b_3 >$ , если :
$a_1 = (1, 2, 1)^T$
$a_2 = (1, 1, -1)^T $
$a_3 = (1, 3, 3) ^T$
$b_1= (2, 3, -1) ^T$
$b_2 = (1, 2, 2) ^T$
$b_3 = (1, 1, - 3) ^T$

2). Разложить вектор $X $на сумму двух векторов, один из которых лежит в подпространстве, натянутом на векторы $a_1, a_2, a_3$ , а другой ортогонален к этому подпространству.
$X = (-3, 5, 9, 3) ^T$

$a_1 = (1, 1, 1, 1)^ T$ $a_2 = (2, - 1, 1, 1) ^T$ $a_3 = (2, - 7, - 1, - 1)^ T$

3) Если линейный оператор φ , действующий в пространстве L n , имеет n линейно независимых собственных векторов e1, e2, … en, соответствующих собственным числам λ1, λ2, …..λn, то в базисе из этих векторов матрица оператора имеет диагональный вид с диагональными элементами, равными собственным числам.
Для заданной матрицы оператора найти этот базис и соответствующую ему диагональную форму матрицы.
$ \left( \begin{array}{cccc} 0 & 1 & 0 & 0 \\ 0 &0 & 1 & 0 \\ 0 & 0 & 0 & 1\\ -6 & 1 & 7 & -1\end{array} \right)$


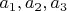
4). Линейный оператор φ переводит векторы $a_1, a_2, a_3$ соответственно в векторы $b_1, b_2, b_3.$
Найти матрицу оператора φ в том же базисе, в котором заданы координатами все векторы:
$a_1 = (1, 2, -3) ^T a_2 = (0, 1, 2)^ T a_3 = (1, 0, 4) ^T$
$b_1= (1, 1, 1)^ T b_2 = (1, 2, 1) ^T b_3 = (0, 1, 1) ^T$

5). Преобразовать к каноническому виду ортогональным преобразованием квадратичную форму и выписать преобразование координат
$x_1_2 + 2x_2_2 + 3x_3_2 - 4x_1x_2 - 4x_2x_3 $

Правильно ли, что в первом задании базис пересечения$ a=(a_1, a_2),$ размерность равна 2
базис суммы будет $b=(b_1,b_2,b_3)$, а размерность суммы равна 3?

Заранее спасибо за любую помощь

[nestoklon]

Есть подозрение, что если вы представите попытки решения, даже совершенно неправильные, но показывающие что вы что-то делали, вам охотно помогут.

[tdk]

Правильно ли, что в первом задании базис пересечения $a=(a_1, a_2)$, размерность равна 2
базис суммы будет $b=(b_1,b_2,b_3),$ а размерность суммы равна 3? я вот сомневаюсь.

базис подпространства $l1$ будет$ a=(a_1,a_2)$, а как это доказать ($a1$ есть сумма $a2$ и $a3$) ? Как записать? => размерность равна 2

базис подпространства $l2 b=(b_1, b_2,b_3 ),$ тоже не знаю как это расписать. => размерность 3

И вот у мне кажется, что сумма $l1$ и $l2 $это $l2 $, а пересечение$ l1$? или размерность суммы это 2+3? как расписать?
Подскажите, пожалуйста

[nestoklon]

tdk в сообщении #150388 писал(а):

а как это доказать (a1 есть сумма a2 и a3) ?

Это именно оно и есть. Вы построили базис размерности два. Значит, пространство двумерно.

tdk в сообщении #150388 писал(а):

тоже не знаю как это расписать. => размерность 3

Рекомендую написать "по определению".

Размерность пересечения/суммы это размерность пересечения/суммы. По определению это размерность базиса соответствующих пространств. Если вы сможете построить в трёхмерном пространтве базис из пяти векторов, это будет круто.

[Really]

tdk в сообщении #150388 писал(а):

базис подпространства l2 b=(b1, b2,b3 ), тоже не знаю как это расписать. => размерность 3

Невооруженным взглядом видно, что система $b$ линейно зависима.
Найдите, скажем, $b_2+b_3$.

tdk в сообщении #150388 писал(а):

И вот у мне кажется, что сумма l1 и l2 это l2 , а пересечение l1? или размерность суммы это 2+3? как расписать?

Вообще, когда у вас есть система из каких-либо $k$ векторов, запишите матрицу по столбцам и найдите Гауссом ее ранг. Вы
вычислите и размерность линейной оболочки, и заодно найдете
какой-нибудь базис.

[tdk]

Как доказать, что именно эти вектора базис? Как расписать, что они линейно независимы?

Добавлено спустя 3 минуты 55 секунд:

to Really
Мне казалось, что вектора b1, b2, b3 линейно независимы

[nestoklon]

tdk в сообщении #150408 писал(а):

Как расписать, что они линейно независимы?

1) По определению. Сами найдёте?
2) Попробовать ортогонализовать их.

[tdk]

Меня вот смущает транспонирование.
Я думаю так:

$ \left( \begin{array}{cc} 1 \\ 2 \\ 1\end{array} \right)$ $x_1$ + $ \left( \begin{array}{cc} 1 \\ 1\\ -1\end{array} \right)$ $x_2 =0$

[Jnrty]

Jnrty:

tdk, перенабираете все формулы по правилам форума. Детали можно посмотреть здесь: http://dxdy.ru/topic183.html (подробно), http://dxdy.ru/topic8355.html (кратко). Если не сделаете, отправлю тему в "Карантин".

[Really]

tdk в сообщении #150408 писал(а):

to Really
Мне казалось, что вектора b1, b2, b3 линейно независимы

Это не так. Я же писал вам: $b_2+b_3=b_1$.

[nestoklon]

Really в сообщении #150424 писал(а):

Это не так. Я же писал вам: $b_2+b_3=b_1$.

Подсказка: $1\cdot b_1+(-1)\cdot b_2+(-1)\cdot b_3=0$

[tdk]

Тогда получается размерность $l2$ тоже равна 2? И базис будет $b=(b_1,b_2)$ ?

[nestoklon]

tdk в сообщении #150437 писал(а):

И базис будет $b=(b_1,b_2)$ ?

Например, так. Можно взять какой-нибудь другой, поудобнее.

[tdk]

А как Вы понимаете, какой поудобнее? И удобнее для чего?
Что-то я совсем запуталась. Так сумма $L1$ и $L2$ все-таки будет равно $L2$, а пересечение $L1$ ?

[Бодигрим]

tdk в сообщении #150447 писал(а):

А как Вы понимаете, какой поудобнее? И удобнее для чего?

Удобнее - субъективно, для дальнейших манипуляций. Обычно удобно выбирать такой, в котором все компоненты малы, или какие-то равны 0.

Добавлено спустя 1 минуту 58 секунд:

tdk в сообщении #150447 писал(а):

Так сумма L1 и L2 все-таки будет равно L2, а пересечение L1?

Аргументация?