Беда с вариационным принципом.

[amon]

Alex-Yu в сообщении #1494458 писал(а):

Вариационное исчисление? Для знающего матан это такая банальность... Ну полистать вечерок учебник (любой). А можно и не листать, из ЛЛ1 все и так ясно.

Эта цитата навеяла воспоминания. Рассмотрим задачу об экранировании внешнего электрического поля электронным газом на поверхности не важно чего. В первом приближении (приближении среднего поля) задача сводится к решению системы уравнений

$$ \begin{align} &-\Psi''+\Phi\Psi=E\Psi\\ &\Phi''= \Psi^2\\ &\Psi(0)=\Psi(\infty)=0\\ &\Phi'(0)=1,\,\Phi'(\infty)=0 \end{align} $$

Для нахождения энергии основного состояния воспользуемся вариационным принципом. Выберем волновую функцию

$$\Psi=2a^\frac{3}{2}xe^{-ax},$$

Сосчитаем потенциал, положив его в нуле нулем:

$$\Phi(x)=\int\limits_{0}^{x}\left(\int\limits_{0}^{y}|\Psi(t)|^2dt-1\right)dy.$$

Получим такую картинку

$$\Phi(x)=\frac{e^{-2 a x} \left(-2 a x (a x+2)+3 e^{2 a x}-3\right)}{8 a^2}$$

Вложение:

.png [ 4.82 Кб | Просмотров: 1725 ]

Сосчитаем функционал энергии

$$H=\int\limits_{0}^{\infty}\left(\Psi'^2(x)+\Phi(x)\Psi^2(x)\right)dx=a^2+\frac{33}{128 a^2}$$

Находим минимум по $a$ и радуемся жизни.

А теперь давайте положим потенциал нулем на бесконечности (поле в нуле останется то же самое):

$$ \begin{align} &\Phi(x)=-\int\limits_{x}^{\infty}\left(\int\limits_{0}^{y}|\Psi(t)|^2dt-1\right)dy\\ &\Phi(x)=-\frac{e^{-2 a x} (2 a x (a x+2)+3)}{8 a^2} \end{align} $$

Вложение:

1.png [ 4.8 Кб | Просмотров: 1725 ]

Считаем $H$ и с изумлением получаем

$$H=a^2-\frac{15}{128 a^2},$$

т.е. никакого минимума у функционала энергии нет. Беря разные значения потенциала на бесконечности можно таким способом получать самые разные энергии основного состояния. С другой стороны, все знают, что от сдвига на константу ничего не должно меняться, разве что начало отсчета энергии сдвинется. Вопрос: что за фигня?

Вопрос обращен к физикам, изучавшим вариационное исчисление по Ландау-Лифшицу. Математики, IMHO, на него мгновенно ответят.

[AnatolyBa]

А вот математики. После того как ответят что за фигня, скажут ли они как правильно? А если скажут, ткнут ли носом в учебник, где это написано? Или придумают сами.
А если придумают сами, будет ли это что-то такое, на что физики (скажем, не очень грамотные математически физики) не способны?

[amon]

AnatolyBa в сообщении #1494831 писал(а):

После того как ответят что за фигня, скажут ли они как правильно? А если скажут, ткнут ли носом в учебник, где это написано?

Скажут. Ткнуть могут, например, в учебник Смирнова. Куда - пока не скажу, что бы интригу не разрушать. Самому тоже можно догадаться, но с напрягом (я в свое время, 40 лет назад, не догадался, но нашел ответ в упомянутом учебнике).

[amon]

Видимо, надо написать подробности, исправить то, что второпях я неправильно написал и дать некие наводящие соображения.
Рассмотрим газ невзаимодействующих электронов, заполняющих полупространство $x\ge 0.$ Электроны болтаются в некотором потенциале $V(x)$ и описываются гамильтонианом

$$\hat{H}=\frac{\hat{p}_x^2+\hat{p}_y^2+\hat{p}_z^2}{2}+V(x)\quad (*).$$

В первом приближении будем считать, что потенциал $V(x)$ это просто $V=e\varphi,$ где $e$ - заряд электрона, а $\varphi$ - электростатический потенциал, удовлетворяющий уравнению Пуассона (приближение Хартри)

$$ \begin{align} &-\varphi''(x)=4\pi e n \Psi^2(x)\\ &-\varphi'(0)=E,\,\varphi'(\infty)=0. \end{align} $$

Здесь $n$ - двумерная плотность электронов, $E$ - внешнее электрическое поле, мы считаем, что все электроны сидят на нижнем уровне гамильтониана $H.$ Можно выбрать единицы измерения так, что все константы в уравнениях превращаются в единицы, учесть, что заряд электрона отрицателен и положить $k_y=k_z=0.$ Тогда получим систему уравнений

$$ \begin{align} &-\Psi''+\Phi\Psi=E\Psi\\ &\Phi''=\Psi^2\\ &\Psi(0)=\Psi(\infty)=0\\ &\Phi'(0)=1,\,\Phi'(\infty)=0 \end{align} $$

(В первом посте у меня было по привычке написано $4\pi$ в Пуассоне, и наврано со знаками в уравнениях, в вычислениях все нормально - виноват.)
Система получилась Лагранжева с действием

$$\int\limits_{0}^{\infty}dx\left(\left\Psi'^2(x)+\Psi^2(x)\Phi(x)-E\Psi^2(x)\right)+\frac{1}{2}\Phi'^2(x)\right)ю$$

Вопрос: каким граничным условиям удовлетворяют экстремали этого функционала?

[AnatolyBa]

Ну что-ж, я шел по этому пути, только запутался в знаках. Хорошо, а то я думал, что совсем уже не соображаю.
Мне кажется (полистал Смирнова), вы намекаете на условие $\Phi(0)=0$ в доплнении к уже написанным. Оно позволяет не заморачиваться членами $\Phi'(0)\delta \Phi(0)$ возникающими при варьировании.
А правилно ли что в лагранжиан входит $E\Psi^2$ ? Не должна ли энергия сама получаться после нахождения функций как $\int\limits_{0}^{\infty}dx\left(\Psi'^2(x)+\Psi^2(x)\Phi(x)\right)$ (при нормировке $\Psi$ на единицу)

[amon]

AnatolyBa в сообщении #1495292 писал(а):

вы намекаете на условие $\Phi(0)=0$ в доплнении к уже написанным.

Я намекаю на то, что стандартная вариационная задача предполагает некоторые стандартные граничные условия.

AnatolyBa в сообщении #1495292 писал(а):

А правилно ли что в лагранжиан входит $E\Psi^2$ ?

В такой постановке $E$ это множитель Лагранжа, который аккурат ставит условие нормировки волновой функции на единицу. Если мы заранее выбрали пробную волновую функцию нормированной, то этот член можно выкинуть.

[amon]

Видимо, пора писать ответ как я его понимаю. Есть у нас вариационная задачка

$$S=\int\limits_{0}^{\infty}dx\left(\left\Psi'^2(x)+\Psi^2(x)\Phi(x)-E\Psi^2(x)\right)+\frac{1}{2}\Phi'^2(x)\right),$$

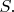
найти экстремаль $S.$ Если к действию ничего не дописывать, то возможны такие варианты: задача с фиксированными концами - зафиксированы значения функции на концах промежутка интегрирования. Для рассматриваемой задачи это условия $\Psi(0)=\Psi(\infty)=0.$ И задача со свободными концами, когда значения искомой функции на концах промежутка вообще не фиксированы. В последнем случае у уравнения Эйлера-Лагранже возникают так называемые естественные граничные условия, которые в рассматриваемой задаче - условие на потенциал в бесконечности - $\left.\frac{\partial \mathcal{L}}{\partial \Phi'}\right|_{x=\infty}=0=\Phi'(\infty).$

Условие $\Phi'(0)=1$ не относится ни к одному из этих стандартных условий, и що з ним робити сходу не понятно. Именно благодаря ему возникает внеинтегральный член, зависящий от значения потенциала в нуле. Мне, в свое время, помог рецепт, подсмотренный в учебнике Смирнова Курс высшей математики т.4 часть 1 глава II, вариационное исчисление, параграф 84, "функционалы более общего типа". Там сказано, что для того, что бы получить задачу с нестандартными условиями на границе можно добавить в функционал член, зависящий от значения функции на границе промежутка интегрирования. Например, функционал $S'[\Phi]=-\Phi(0)+S$ при стандартной процедуре $\left.\frac{\partial}{\partial\alpha}S'[\Phi+\alpha h]\right|_{\alpha=0}$ выдаст после интегрирования по частям внеинтегральный член $(\Phi'(0)-1)h(0),$ что и даст нужное граничное условие.

Возвращаясь к исходной задаче, вышеописанное означает, что надо писать функционал как

$$-\Phi(0)+\int\limits_{0}^{\infty}dx\left(\left\Psi'^2(x)+\Psi^2(x)\Phi(x)-E\Psi^2(x)\right)+\frac{1}{2}\Phi'^2(x)\right),$$

внеинтегральный член на нормированных пробных функциях $\int\limits_{0}^{\infty}\Psi^2(x)dx=1$ загоняется под интеграл, и получается

$$\int\limits_{0}^{\infty}dx\left(\left\Psi'^2(x)+\Psi^2(x)\left(\Phi(x)-\Phi(0)\right)-E\Psi^2(x)\right)+\frac{1}{2}\Phi'^2(x)\right),$$

т.е правильный ответ будет если положить потенциал в нуле нулем. Я это к тому, что изучение вариационного исчисления "по Ландау-Лифшицу" дает прекрасную возможность наступить даже на слабо замаскированные грабли.