Математическое ожидание площади треугольника

[marie-la]

В треугольник единичной площади бросается три точки (с равномерным распределением их положения по площади треугольника) - найти математическое ожидание площади треугольника, образованного этими тремя точками.

Я знаю ответ $\frac{1}{12}$. Пыталась поступить так - зафиксировать прямую, на которой две из трех точек, и третью равномерно кинуть в получившийся треугольник и четырехугольник. Там получается выражение с площадями двух частей, и не понимаю, что с ним дальше делать :(

[Aritaborian]

Читали, что по этому поводу написано на MathWorld?

[marie-la]

Aritaborian
Хочется чего-то попроще, чтоб решение записать можно было.

[DeBill]

marie-la
Ну, ручками - можно сделать. Но - длинно, в 6 шагов. И один интеграл (однократный) все же пришлось считать.
Если интересно - напишите, я схему набросаю...

[marie-la]

DeBill
Попробую сама расписать, раз вы говорите, что там считается.

[DeBill]

marie-la
Ну, схема довольно замысловатая - однако проще я не вижу...
Пусть наш тр-к имеет площадь $S=1$, и $p$ - ожидаемая площадь треугольника из трех брошенных точек. Тогда
1. Счет $p$: Отрежем от нашего тр-ка прямой, параллельной основанию, и делящую его высоту в отношении $(1-\delta) : \delta$, узкую полоску. Тогда из формулы для условного матожидания имеем (с точностью до малых второго порядка): $p=((1-\delta)^2)^3\cdot p(1-\delta)^2+3\cdot 2\delta \cdot q$, где $q$ - ожидаемая площадь для случая, когда одна точка равномерно распределена на стороне тр-ка, а две других - равномерно по всему тр-ку ($(1-\delta)^2$ - площадь оставшегося тр-ка, а также и вероятность в него попасть точке; в кубе - потому как точек три; $2\delta$ - 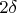площадь полоски; 3 - потому как одна из трех могла попасть в полоску). Сравнивая в этом равенстве малые первого порядка, получим

$$4p=3q$$

2. Аналогично, отрезая полоску сбоку, получим

$$7q=r+4s$$

где $s$- ожидаемая площадь для случая "одна точка - равномерномерно на стороне, другая - на другой стороне, третья - в тр-ке", а $r$- ожидаемая площадь для случая "одна точка - в вершине, две - в тр-ке"
3. Аналогично получаем $3s=t+u$, где $t$- для случая "три точки бегают по трем сторонам", а $u$ - "одна - в вершине, другая - на основании, третья - в тр-ке".
4. Аналогично $2u=3r$
5. $t=\frac{1}{4}$- можно получить "вычитанием" площадей, а
6. $u=\frac{2}{9}$ - - интегрированием (используя простой факт, что в случае "одна точка - вершина, другая - вершина, третья - в тр-ке", ожидаемая площадь равна одной трети - ибо свойство медиан...)
Аккуратный счет теперь даст желаемый ответ...
Нда.....

[Aritaborian]

DeBill, а что насчёт интеграла, который приводится в упомянутой мною статье энциклопедии MathWorld? Там упоминается некая cylindrical algebraic decomposition. Ваш способ, насколько я способен понять, принципиально является более простым?

[bigredcat]

marie-la в сообщении #1492801 писал(а):

В треугольник единичной площади бросается три точки (с равномерным распределением их положения по площади треугольника) - найти математическое ожидание площади треугольника, образованного этими тремя точками.

Я знаю ответ $\frac{1}{12}$. Пыталась поступить так - зафиксировать прямую, на которой две из трех точек, и третью равномерно кинуть в получившийся треугольник и четырехугольник. Там получается выражение с площадями двух частей, и не понимаю, что с ним дальше делать :(

По Монте-Карло посчитать. Программка пишется за пять минут.

[Aritaborian]

bigredcat, программка программкой, но в данном случае речь идёт об аналитическом нахождении искомой величины. Не путайте тёплое с мягким.

[DeBill]

Aritaborian
Да скорее всего, вычисление того интеграла и даст рассмотренную схему (переходы к "граничным" значениям сл. величин соответствуют, типа, подстановке пределов интегрирования в первообразную; интеграл - 6-мерный, ну и тут тоже 6...).
А вот попытки использования симметрий - как в знаменитой задаче про лягушку (лягушка прыгает на метр в случайном направлении. Найти вероятность того, что за три прыжка она ускачет не далее чем на метр от начальной точки), или - тоже классика "на $n$- мерной сфере выбрали $n+2$ точки. Найти вероятность того, что их выпуклая оболочка содержит центр сферы" - чёто не прокатили...