1997:
9988: 0+4994*2,! 1100+4444*2
18887: 1111+8888*2,!
97768: 0+48884*2,! 1000+48384*2 10100+43834*2 11100+43334*2
184547: 11011+86768*2,!
930028: 1100+464464*2,! 110000+410014*2
1750067: 1111+874478*2 110011+820028*2,!
9350638: 1110+4674764*2 110110+4620264*2,!
17711177: 1+8855588*2 10001+8850588*2 1010101+8350538*2,! 11111111+3300033*2
94822948: 0+47411474*2,! 10000100+42411424*2
179745797: 100001+89822898*2 10100101+84822848*2,! 111101111+34322343*2
977293768: 0+488646884*2,! 1010000+488141884*2 10001000+483646384*2 11011000+483141384*2 100000100+438646834*2 101010100+438141834*2 110001100+433646334*2 111011100+433141334*2
1844686547: 110101011+867292768*2,!
9301551028: 10000100+4645775464*2,! 1000010000+4150770514*2 1100011000+4100770014*2
17503102067: 11111111+8745995478*2 1100000011+8201551028*2,!
93523232638: 11101110+46756065764*2 111111110+46706060764*2 1101010110+46211111264*2,!
177146465177: 100000001+88523232588*2 10100000101+83523232538*2,! 111100001111+33023232033*2
948711106948: 0+474355553474*2,! 11000000+474350053474*2 100100000+474305503474*2 111100000+474300003474*2 100000000100+424355553424*2 100011000100+424350053424*2 100100100100+424305503424*2 100111100100+424300003424*2
1798312224797: 1001111001+898655556898*2 101110011101+848601106848*2,!
9772534363768: 1110000+4886266626884*2 11110000+4886261626884*2 110110000+4886212126884*2,!
18446168716547: 1101100011011+8672534352768*2,!
93007954881028: 101000010100+46453477435464*2,!
175026800851067: 111001100111+87457899875478*2 11011111111011+82007844870028*2,!
935184809471638: 110000000110+467537404735764*2 11110000011110+462037404730264*2,!
1771359717953177: 1+885679858976588*2 100000001+885679808976588*2 1000100010001+885179808971588*2 101010101010101+835174808471538*2,! 1111111111111111+330124303421033*2
9484956897484948: 0+4742478448742474*2,! 10010000000+4742473443742474*2 100001000000+4742428448242474*2 110011000000+4742423443242474*2 1000000000000100+4242478448742424*2 1000010010000100+4242473443742424*2 1000100001000100+4242428448242424*2 1000110011000100+4242423443242424*2
17979804884079797: 1010111111110101+8484846886484848*2,!
97776853724977768: 0+48888426862488884*2,! 1000000000+48888426362488884*2 10100000000+48888421812488884*2 11100000000+48888421312488884*2 10000000100000+48883426862438884*2 10001000100000+48883426362438884*2 10010100100000+48883421812438884*2 10011100100000+48883421312438884*2 100000000010000+48838426862483884*2 100001000010000+48838426362483884*2 100010100010000+48838421812483884*2 100011100010000+48838421312483884*2 110000000110000+48833426862433884*2 110001000110000+48833426362433884*2 110010100110000+48833421812433884*2 110011100110000+48833421312433884*2 1000000000001000+48388426862488384*2 1000001000001000+48388426362488384*2 1000010100001000+48388421812488384*2 1000011100001000+48388421312488384*2 1010000000101000+48383426862438384*2 1010001000101000+48383426362438384*2 1010010100101000+48383421812438384*2 1010011100101000+48383421312438384*2 1100000000011000+48338426862483384*2 1100001000011000+48338426362483384*2 1100010100011000+48338421812483384*2 1100011100011000+48338421312483384*2 1110000000111000+48333426862433384*2 1110001000111000+48333426362433384*2 1110010100111000+48333421812433384*2 1110011100111000+48333421312433384*2 10000000000000100+43888426862488834*2 10000001000000100+43888426362488834*2 10000010100000100+43888421812488834*2 10000011100000100+43888421312488834*2 10010000000100100+43883426862438834*2 10010001000100100+43883426362438834*2 10010010100100100+43883421812438834*2 10010011100100100+43883421312438834*2 10100000000010100+43838426862483834*2 10100001000010100+43838426362483834*2 10100010100010100+43838421812483834*2 10100011100010100+43838421312483834*2 10110000000110100+43833426862433834*2 10110001000110100+43833426362433834*2 10110010100110100+43833421812433834*2 10110011100110100+43833421312433834*2 11000000000001100+43388426862488334*2 11000001000001100+43388426362488334*2 11000010100001100+43388421812488334*2 11000011100001100+43388421312488334*2 11010000000101100+43383426862438334*2 11010001000101100+43383426362438334*2 11010010100101100+43383421812438334*2 11010011100101100+43383421312438334*2 11100000000011100+43338426862483334*2 11100001000011100+43338426362483334*2 11100010100011100+43338421812483334*2 11100011100011100+43338421312483334*2 11110000000111100+43333426862433334*2 11110001000111100+43333426362433334*2 11110010100111100+43333421812433334*2 11110011100111100+43333421312433334*2
184554796460845547: 11001111011110011+86776842724867768*2,!
930102861158301028: 1010110011010100+464546375573645464*2,!
1750206712326502067: 110001010010100011+820102851158201028*2,!
9352262944502522638: 1111011111011110+4675575966695755764*2 110010100010100110+4621126422246211264*2,!
17714514998995145177: 10000100100100001+8852257449447522588*2 1010010110110100101+8352252444442522538*2,!
94868674988936686948: 1011010000000+47434336988963343474*2,!
179837338977884373797: 10100011000011000101+84868663988936686848*2,!
977210827757718112768: 100110000011001000+488555358878853555884*2,!
1844422645515446125547: 110001010000010100011+867210817757718012768*2,!
9299639090670908370028: 11010000000000101100+4644314545335454134464*2,!
17500377181431817739957: 1011101000110001011101+8244638090660908364428*2,!
93494148994849995040528: 11000110001100011000+46741574442424447514764*2,!
175998208989699979189967: 11110111000000011101111+82444048994849984044428*2,!
945980188986689782089538: 10011111011110111110010+467984538987789835489764*2,!
1781960476973379663179087: 110000101000000101000011+835980187986689781089538*2,!
9591674146707176403870958: 100011011000001101100010+4745831567853587651385474*2,!



![$[2,0,0,2,0,4,0,0,0,0]:18211171=[11100111]+[03555530]\cdot2$ $[2,0,0,2,0,4,0,0,0,0]:18211171=[11100111]+[03555530]\cdot2$](https://dxdy-01.korotkov.co.uk/f/c/7/7/c77dd2e751b3100761493fcac2e1094b82.png)
 , где 101 и 787 одинаковой длины, первая программа нашла.
, где 101 и 787 одинаковой длины, первая программа нашла. ,здесь первая программа выдала двоичное число длиной меньше найденного палиндрома, не дойдя до результата
,здесь первая программа выдала двоичное число длиной меньше найденного палиндрома, не дойдя до результата  .
. , не дойдя до результата
, не дойдя до результата  .
. .
. и т.д.
и т.д. и палиндромов весьма специального вида)? Мне это как-то совсем не очевидно. Этот вопрос кем-то исследовался? Может исходный постулат о существовании таких палиндромов
и палиндромов весьма специального вида)? Мне это как-то совсем не очевидно. Этот вопрос кем-то исследовался? Может исходный постулат о существовании таких палиндромов  .
. ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.








 ,
,  ,
,  ,
,  ,
,  (отличается),
(отличается),  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. не палиндром.
не палиндром.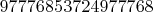 :
: .
. ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. .
.