Теперь мы рассмотрим сильно аддитивные арифметические функции

, которые удовлетворяют условиям, что для всех простых значений

выполняется

и дисперсия арифметической функции

.
Напомним, что при выполнении условий:

и

сильно аддитивная арифметическая функция

при

имеет предельным нормальное распределение.
Нам известно (17), что для среднего значения любой сильно аддитивной арифметической функции

при

выполняется:

.
Учитывая, что

, в данном случае значение

.
Теперь определим дисперсию

при

.
Для

при

, если

выполняется:

.
Так как

, то дисперсия

при

на основании свойств дисперсии:
![$D_n[g] \sim -\sum_{p \leq n} \frac {g(p)}{p}$ $D_n[g] \sim -\sum_{p \leq n} \frac {g(p)}{p}$](https://dxdy-01.korotkov.co.uk/f/4/6/9/46922319c5c36f3e3cb70a192253ce6782.png)
. (20)
Теперь докажем следующее утверждение.
Утверждение 2
Пусть для сильно-аддитивной арифметической функции

для всех простых значений

выполняется

и дисперсия
![$D_n[g] \to \infty,n \to \infty$ $D_n[g] \to \infty,n \to \infty$](https://dxdy-03.korotkov.co.uk/f/2/e/9/2e9ca416f936b397e9c16edd95cac54d82.png)
. Тогда асимптотики всех нечетных центральных моментов для сильно-аддитивной арифметической функции

равны:

, (21)
а асимптотики всех четных центральных моментов для сильно-аддитивной арифметической функции

равны:

. (22)
Доказательство
Пусть случайная величина

принимает два значения:

с вероятностью

и

с вероятностью

.
Тогда среднее значение и дисперсия

соответственно равны:
![$E[X_p]=\frac {g(p)}{p},D[X_p]=\frac {|g(p)|}{p}-\frac {g^2(p)}{p^2}=-\frac {g(p)}{p}-\frac {g^2(p)}{p^2}$ $E[X_p]=\frac {g(p)}{p},D[X_p]=\frac {|g(p)|}{p}-\frac {g^2(p)}{p^2}=-\frac {g(p)}{p}-\frac {g^2(p)}{p^2}$](https://dxdy-04.korotkov.co.uk/f/f/8/1/f81fe5352e2e856497c829e53ce3657c82.png)
.
Построим случайную величину

, где

- независимы. Тогда среднее значение и дисперсия
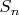
соответственно равны:
![$E[S,n]=\sum_{p \leq n} \frac {g(p)}{p},D[S,n]=-\sum_{p \leq n} \frac {g(p)}{p}-\sum_{p \leq n} \frac {g^2(p)}{p^2}$ $E[S,n]=\sum_{p \leq n} \frac {g(p)}{p},D[S,n]=-\sum_{p \leq n} \frac {g(p)}{p}-\sum_{p \leq n} \frac {g^2(p)}{p^2}$](https://dxdy-02.korotkov.co.uk/f/1/b/6/1b647a4314f6075eb4e8010d4a6befd382.png)
.
На основании Центральной предельной теоремы случайная величина
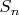
имеет предельным нормальное распределение.
Учитывая, что

, то ряд

- сходится. Поэтому
![$D[S,n]=-\sum_{p \leq n} \frac {g(p)}{p}+O(1)$ $D[S,n]=-\sum_{p \leq n} \frac {g(p)}{p}+O(1)$](https://dxdy-02.korotkov.co.uk/f/d/4/8/d48bfdc5775239bd4fe4cb47182ab4ce82.png)
.
Следовательно, при

получаем
![$A_n \to E[S,n],D_n \to D[S,n]$ $A_n \to E[S,n],D_n \to D[S,n]$](https://dxdy-02.korotkov.co.uk/f/d/d/0/dd02eb37608e28e4aeb4c88614b0e06482.png)
, поэтому совпадают предельные нормальные распределения сильно аддитивной арифметической функции

и случайной величины
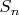
.
Отсюда вытекает, что совпадают все остальные вероятностные характеристики (в том числе центральные моменты более высоких порядков) сильно аддитивной арифметической функции

и случайной величины
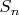
. Поэтому для нахождения центральных моментов более высоких порядков для сильно аддитивной арифметической функции

достаточно найти центральные моменты для случайной величины
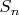
, чем мы и займемся.
Сначала определим центральные моменты

-ого порядка для случайной величины

:
![$E[(X_p- \frac {g(p)}{p})^k]=E[{X_p}^k]-\frac {kg(p)}{p}E[{X_p}^{k-1}]+...+(-1)^k \frac {g^k(p)}{p^k}=$ $E[(X_p- \frac {g(p)}{p})^k]=E[{X_p}^k]-\frac {kg(p)}{p}E[{X_p}^{k-1}]+...+(-1)^k \frac {g^k(p)}{p^k}=$](https://dxdy-03.korotkov.co.uk/f/a/4/1/a41a423ff6f2af88888b136fdd2abde782.png)

.
Поэтому центральные моменты

-ого порядка для случайной величины
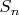
и соответственно

при

равны:

.
При нечетном

, так как

, то получим:

, что соответствует (21).
При четном

, так как

, то получим:

, что соответствует (22).
На основании материалов темы об асимптотике сумм функций простых чисел приведем анализ асимптотики выражения

при условии, что

.
1. Если

, где

, то асимптотика суммы:

.
2. Если

монотонно убывает и

, то асимптотика суммы:

.
3. Если

монотонно возрастает, как

или медленнее, то асимптотика суммы равна:

или убывает медленнее.
4. Если

монотонно возрастает, как

или быстрее, то ряд:

- сходится.
Поэтому условиям

и
![$D_n[g]=-\sum_{p \leq n} \frac {g(p)}{p} \to \infty,n \to \infty$ $D_n[g]=-\sum_{p \leq n} \frac {g(p)}{p} \to \infty,n \to \infty$](https://dxdy-01.korotkov.co.uk/f/0/e/4/0e4bf777cbef78cf4630103f6e27963282.png)
удовлетворяют случаи 1-3.
Ваши новые посты сложноваты для проверки, но вполне возможно, по сути верны. Хотя, возможно, требуют более строгих доказательств.
Мне кажется, что последние сообщения не являются сложными с точки зрения теории вероятностей и утверждения доказаны строго. Здесь главное идея метода оценки моментов арифметических функций.