Кубилюс расширяет класс сильно аддитивных функций и рассматривает класс H арифметических функций.
Пусть

и

- последовательность целых положительных степеней простых чисел, такая что:

- сходится (6).
Определим другую аддитивную функцию

, полагая

для всех

, отличных от

. Для чисел

пусть

- пробегает любые значения. Тогда предельные законы:

и

существуют и совпадают.
В частности в качестве

можно взять сильно аддитивную арифметическую функцию, связанную с

соотношением

для всех простых

при

.
Рассмотрим арифметические функции, которые, как было доказано Кубилюс, относятся к классу

.
Арифметическая функция количества делителей числа

с учетом кратности -

. Данная арифметическая функция при всех простых значениях

совпадает с сильно аддитивной функцией

, т.е.

. Поэтому совпадают асимптотики среднего значения и дисперсии
![$E[\Omega,n]=D[\Omega,n] \to \ln\ln(n)+O(1)$ $E[\Omega,n]=D[\Omega,n] \to \ln\ln(n)+O(1)$](https://dxdy-04.korotkov.co.uk/f/3/8/1/381b813e2f22b9915b982b0bc468b6fd82.png)
.
Учитывая, что арифметическая функция

при

стремится к нормальному распределению с аналогичными характеристиками, как сильно аддитивная функцией

, то совпадают все остальные характеристики арифметических функций. Поэтому асимптотики всех центральных моментов арифметической функции

также равны

.
Арифметические функции количества простых делителей, находящихся на последовательностях

соответственно:

также имеют предельными нормальное распределение с асимптотикой средних значенией и дисперсий равными

. Поэтому совпадают все остальные характеристики данных арифметических функций, включая центральные моменты высоких порядков.
Для последовательностей случайных величин, которые мы строим, оставим старые обозначения. Рассмотрим случайную величину

, принимающую два значения:

с вероятностью

и

с вероятностью

. Тогда среднее значение
![$E[x_p]=1/2p$ $E[x_p]=1/2p$](https://dxdy-03.korotkov.co.uk/f/2/4/f/24f3f405f6e29bbadc19ee9cdb5fb19d82.png)
и дисперсия
![$D[X_p]=1/2p-1/4p^2$ $D[X_p]=1/2p-1/4p^2$](https://dxdy-03.korotkov.co.uk/f/e/e/0/ee09fc720a15123d2a0f0fc9a09b128a82.png)
.
Построим случайную величину

, где

- независимые случайные величины. Тогда асимптотики среднего значения и дисперсии данной случайной величины соответственно равны:
![$E[S,n]=1/2\sum_{p \leq n} {1/p}=1/2 \ln\ln(n)+O(1)$ $E[S,n]=1/2\sum_{p \leq n} {1/p}=1/2 \ln\ln(n)+O(1)$](https://dxdy-03.korotkov.co.uk/f/6/a/a/6aaed9e36a7b75fd080310da6409df5b82.png)
,
![$D[S,n]=1/2\sum_{p \leq n} {1/p}-1/4\sum_{p \leq n} {1/p^2}=\ln\ln(n)+O(1)$ $D[S,n]=1/2\sum_{p \leq n} {1/p}-1/4\sum_{p \leq n} {1/p^2}=\ln\ln(n)+O(1)$](https://dxdy-04.korotkov.co.uk/f/3/4/0/340e5df0afe4f77d06edf8863ec61ff282.png)
, так как ряд

- сходится.
Таким образом, среднее значение, дисперсия и их асимптотики у последовательности случайных величин

совпадают со средним значением, дисперсией и асимптотикой арифметических функций

при

. Учитывая, что последовательность случайных величин

на основании ЦПТ также стремится к нормальному распределению, как арифметические функции

при

, то предельные функции распределения у них совпадают, а следовательно совпадают все остальные характеристики.
Определим асимптотики центральных моментов более высоких порядков у арифметических функций

при

.
Сначала определим асимптотику центральных моментов

-ого порядка случайной

:
![$E[(X_p-1/2p)^k]=(1-1/2p)^k \frac {1}{2p}+(-1/2p)^k(1-1/2p)=1/2p+O(1/p^2)$ $E[(X_p-1/2p)^k]=(1-1/2p)^k \frac {1}{2p}+(-1/2p)^k(1-1/2p)=1/2p+O(1/p^2)$](https://dxdy-03.korotkov.co.uk/f/6/e/4/6e4f47bcec770632bb2177f7ee04586582.png)
.
Теперь определим асимптотику центральных моментов

-ого порядка случайной
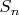
:
![$\sum_{p \leq n} {E[(X_p-1/2p)^k]}=\sum_{p \leq n} {1/2p}+O(\sum_{p \leq n} {1/p^2})=1/2\ln\ln(n)+O(1)$ $\sum_{p \leq n} {E[(X_p-1/2p)^k]}=\sum_{p \leq n} {1/2p}+O(\sum_{p \leq n} {1/p^2})=1/2\ln\ln(n)+O(1)$](https://dxdy-04.korotkov.co.uk/f/3/7/1/371fe3989f778f29a5056710a4e912d882.png)
, (7) так как ряд

- сходится.
Рассмотрим еще одну аддитивную арифметическую функцию

. Доказано, что данная арифметическая функция имеет предельным при

нормальное распределение со средним значением равным 0 и дисперсией

.
Определим асимптотики центральных моментов более высоких порядков у арифметической функции

при

.
В качестве

рассмотрим случайную величину, принимающее значение

с вероятностью

и значение

с вероятностью

.
Тогда среднее значение
![$E[X_p]=0$ $E[X_p]=0$](https://dxdy-01.korotkov.co.uk/f/4/f/7/4f7529509318600ef3457f7b44dc66aa82.png)
, а дисперсия
![$D[X_p]=E[X_p^2]=1/2(\frac{1}{2p}+\frac{1}{2p})=\frac{1}{2p}$ $D[X_p]=E[X_p^2]=1/2(\frac{1}{2p}+\frac{1}{2p})=\frac{1}{2p}$](https://dxdy-01.korotkov.co.uk/f/0/7/7/077d947e8baf4f92136c260796f7496e82.png)
.
Возьмем в качестве случайной величины

, где все

независимы.
Тогда среднее значение
![$E[S,n]=0$ $E[S,n]=0$](https://dxdy-01.korotkov.co.uk/f/4/b/3/4b326f1995cb4e02b0a6d07121d2f0f582.png)
, а дисперсия
![$D[S,n]=\sum_{p \leq n} {\frac{1}{2p}}=0,5\ln\ln(n)+O(1)$ $D[S,n]=\sum_{p \leq n} {\frac{1}{2p}}=0,5\ln\ln(n)+O(1)$](https://dxdy-03.korotkov.co.uk/f/e/7/4/e74115544b65d8f6e565389e30c3c0a882.png)
, т.е равны среднему значению и дисперсии арифметической функции

при

.
Учитывая, что на основании ЦПТ последовательность случайных величин

стремится к нормальному распределению при

, предельные распределения последовательности случайных величин

и арифметической функции

совпадают, а следовательно совпадают асимптотики всех их харектиристик.
Определим асимптотики центральных моментов более высоких порядков у арифметической функции

при

.
Сначала определим асимптотику центральных моментов

-ого порядка случайной

:
![$E[(X_p)^k]=1/2((\frac {1}{\sqrt{2p}})^k+(-\frac {1}{\sqrt{2p}})^k)$ $E[(X_p)^k]=1/2((\frac {1}{\sqrt{2p}})^k+(-\frac {1}{\sqrt{2p}})^k)$](https://dxdy-01.korotkov.co.uk/f/4/f/9/4f954e2f6f4ddfa48e38484ca56790af82.png)
.
При нечетном

значение
![$E[(X_p)^k]=0$ $E[(X_p)^k]=0$](https://dxdy-01.korotkov.co.uk/f/8/0/d/80d3759d78c6282a524b36f59ae7964c82.png)
, а при четном

значение
![$E[(X_p)^k]=(1/2p)^{k/2}$ $E[(X_p)^k]=(1/2p)^{k/2}$](https://dxdy-02.korotkov.co.uk/f/d/e/6/de6330f086eb80928f53708158e1f93282.png)
.
Теперь определим асимптотику центральных моментов

-ого порядка случайной
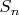
.
При нечетном

значение
![$E[(S_n)^k]=0$ $E[(S_n)^k]=0$](https://dxdy-03.korotkov.co.uk/f/e/6/7/e67053461cbf85cfb0d0ec8cd07a4d4282.png)
, а при четном

значение
![$E[(S_n)^k]=\sum_{p \leq n} {(1/2p)^{k/2}}$ $E[(S_n)^k]=\sum_{p \leq n} {(1/2p)^{k/2}}$](https://dxdy-01.korotkov.co.uk/f/4/e/3/4e363d2ac63221a7d975a02650d668e782.png)
. При

-
![$D[S,n]=\sum_{p \leq n} {(1/2p)}=0,5\ln\ln(n)+O(1)$ $D[S,n]=\sum_{p \leq n} {(1/2p)}=0,5\ln\ln(n)+O(1)$](https://dxdy-04.korotkov.co.uk/f/7/9/e/79ee9a8511ced747fdfe7bc40f65741782.png)
.
При

-
![$E[(S_n)^k]=\sum_{p \leq n} {(1/2p)^{k/2}}=O(1)$ $E[(S_n)^k]=\sum_{p \leq n} {(1/2p)^{k/2}}=O(1)$](https://dxdy-01.korotkov.co.uk/f/0/8/b/08bf346478edacc40a1f52626fd8d24b82.png)
, так как при

ряд

- сходится.