Придумал конструкцию, связанную с порядком

[arseniiv]

Придумал ещё на днях штуку, частными случаями которых будут линейные порядки, циклические порядки, возможно все частичные те и те, а также какие-нибудь страшные штуки типа прямой, к которой в стратегических местах приклеили циклы (можно дискретные). Неформально это множество, покрытое (линейными) промежутками, притом согласованно. (Хотя можно допустить промежутки, идущие в разные стороны, но это уже всё больше пахнет топологией.)

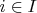
Формализовать я это пытался так: пусть к нашему множеству $X$ прилагается ещё подмножество $I$ отображений в $X$ из линейных порядков, взятых с точностью до изоморфизма. Когда $i\in I$, будем говорить, что $i$ — путь в $X$. Для краткости $D i := \operatorname{dom} i$ (произвольный представитель класса эквивалентности, покуда от него не потребуется чего-то, не переносимого на любой другой из них). Потребуем такое:

1. Если $i$ путь, $p\in D i$, то $i|_{\{x\in D i\mid p <\!\!\!\!> x\}}$ тоже путь, где $<\!\!\!\!>$ — любое из отношений ${<},{\leqslant},{>},{\geqslant}$ на $D i$.

Хочется сделать вместо этого что-то такое:

1x. Если $J\subset I$, то каким-то образом построенное пересечение всех $i\in J$ — тоже путь.

Но уже два в обычном топологическом смысле пути на ориентированном круге, пересекающиеся по несвязному множеству из двух отрезочков, рушат все надежды.

2. Если $i_1, i_2$ пути, притом $D i_1$ имеет наибольший элемент $p_1$, а $D i_2$ наименьший элемент $p_2$ и притом $i_1(p_1) = i_2(p_2)$, то отображение $i$, естественным образом определённое на склеивании $D i_1$ и $D i_2$ (выберем их не пересекающимися) по $p_1, p_2$ (с доопределением порядка), тоже путь. Обозначим его $i_1 + i_2$.

3. Для всякого пути $i = i_1 + i_2 + i_3$, ограничение $i|_{D i\setminus D i_2}$ — путь только в случае $i = i_2 + i_3$ или $i = i_1 + i_2$.

4. Существует путь, образом которого является всё $X$.

Нет, это я хватанул! Представим прямую, разветвляющуюся на две с какой-то точки. Её хочется считать так обобщённо упорядоченной, но одним путём её не накроешь.

4. Существует $I_0\subset I$ такое, что $X = \bigcup_{i\in I_0} \operatorname{im} i$. Избыточно когда верно (4а). С другой стороны может быть надо исключить из $I_0$ пути, о которых говорит (4а), и потребовать в таком виде — но тогда мы потеряем одноточечный порядок, а все обычные порядки хотелось бы оставить как частные случаи этих новых.

4а. [Избыточно в присутствии (1), но (1) мне немного не нравится] Существует путь с пустым образом и пути с образами $\{x\}$ для всех $x\in X$.

5. Если $i$ — путь и $i'$, отличающееся обращением порядка на области определения, тоже путь, то $i$ одноточечный или пустой путь. (Это если нам нужна согласованность, как я изначально хотел.)

Боюсь, что (3) всё равно сформулировано криво (это аж вторая идея, которая для формулировки «непрерывности промежутка» пришла мне в голову).

В формализации я сначала думал, что пути должны быть «строго монотонными» в смысле, что в $I$ не допускаются постоянные функции из множества с более чем одним элементом, но потом передумал, и потом снова передумал и не уверен, что аксиомы выше не позволяют лишнего. Строгая монотонность хороша тем, что достаточно воспринимать пути (как «обобщённо упорядоченные» подмножества $X$) с точностью до изоморфизма их областей определения, а для нестрогой монотонности придётся добавлять ещё оговорки.

Видели где-нибудь что-то подобное? И как это можно довести до ума? Насколько страшные объекты могут быть моделями этого? (Те, которые значительно страшнее, чем большущие ординалы или какие-то большие странные частичные порядки.)

-- Ср окт 28, 2020 01:04:53 --

То есть $I$ — это «атлас путей», где каждый путь — это вложение линейного порядка в $X$.

[Утундрий]

(Оффтоп)

$>$ - более,
$<$ - менее,
$<\!\!\!\!>$ - более-менее.

[arseniiv]

(Оффтоп)

Надо взять на заметку, хорошее чтение.

[Утундрий]

А не отыщется ли в дебрях сего местечка для интервальной арифметики?

[arseniiv]

Ну, интервалы на прямой это же просто интервалы на прямой (будь она хоть и $\mathbb R$), для них наверно не нужно настолько обобщать… Хотя вот при делении на интервал, содержащий ноль, когда получается ерунда, её можно было бы захотеть как-то по-другому выразить, чтобы была не такой ерундой, но я такие вложения интервалов не предполагал, хм.

А, ну давайте рассмотрим тогда пути (обычные) на $\mathbb R\mathrm P^1$, да. Мы их можем подвергать там проективным преобразованиям, в том числе обращению, хотя их ориентация будет иногда меняться (при обращении разумеется всегда). Но такие «промежутки на окружности» опять же можно формализовать не паля из пушек. Но имелись в виду они?